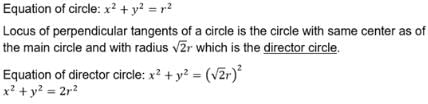Test: Conic Sections - 1 - Commerce MCQ
25 Questions MCQ Test Mathematics (Maths) Class 11 - Test: Conic Sections - 1
If the line 2x – y + λ = 0 is a diameter of the circle x2+y2+6x−6y+5 = 0 then λ =
Length of common chord of the circles x2+y2+2x+6y = 0 and x2+y2−4x−2y−6 = 0 is
Circumcentre of the triangle, whose vertices are (0, 0), (6, 0) and (0, 4) is
The length of the chord joining the point (4 cos θ, 4 sin θ) and 4 (cos(θ+60o), 4 sin(θ + 60o)) of the circle x2+y2 = 16 is
Two perpendicular tangents to the circle x2+y2 = r2 meet at P. The locus of P is
The number of tangents to the circle x2+y2−8x−6y+9 = 0, which pass through the point (3, - 2), is
The value of k, such that the equation = 2x2+2y2−6x+8y+k = 0 represents a point circle, is
The equation ax2+by2+2hxy+2gx+2fy+c = 0 represents a circle only if
x2+y2−6x+8y−11 = 0 is a circle. The points (0, 0) and (1, 8) lie
The length of tangent from the point (2, - 3) to the circle 2x2+2y2 = 1 is
Which one of the following lines is farthest from the centre of the circle x2+y2 = 10?
Which of the following lines is a normal to the circle (x−1)2+(y−2)2 = 10
A circle with its centre on the line y = x + 1 is drawn to pass through the origin and touch the line y = x + 2. The centre of the circle is
Four distinct points (2λ,3λ),(1,0),(0,1) and (0, 0) lie on a circle for
The locus of the point of intersection of the lines x cos α + y sin α = a and x sin α - y cos α = b is
The line y = m x + c is a normal to the circle x2+y2+2gx+2fy+c = 0 if
The equations x = a cos θ + b sin θ , and y = a sin θ − b cos θ y = a sin θ − b cos θ , 0 ≤ θ ≤ 2 π represent
The number of points which have the same power w.r.t. two (different) concentric circles is
A circle passes through (0, 0) ( a, 0), (0, b). The coordinates of its centre are
|
75 videos|238 docs|91 tests
|