Test: Constructions - 2 - SSS 1 MCQ

To divide a line segment AB in the ratio 5 : 7, first a ray AX is drawn so that ∠BAX is an acute angle and then at equal distances points are marked on the ray AX such that the minimum number of these points is

To divide a line segment AB in the ration 4 : 7, a ray AX is drawn first such that ∠BAX is an acute angle and then points A₁,A₂,A₃,…. are located at equal distances on the ray AX and the point B is joined to

A line segment drawn perpendicular from the vertex of a triangle to the opposite side is called the

To divide line segment AB in the ratio A : b ( a, b are positive integers), draw a ray AX so that ∠BAX is an acute angle and then mark points on ray AX at equal distances such that the minimum number of these points is

To divide a line segment AB in the ration 5 : 6, draw a ray AX such that ∠BAX is an acute angle, then draw a ray BY parallel to AX and the points A₁,A₂,A₃… and B₁,B₂,B₃.... are located at equal distances on ray AX and BY, respectively. Then, the points joined are

To divide a line segment AB in the ration 2 : 3, first a ray AX is drawn so that ∠BAX is an acute angle and then at equal distances, points are marked on the ray AX, such tha the minimum number of these points is

To divide a line segment AP in the ration 2 : 9, a ray AX is drawn first such that ∠BAX is an acute angle and then points A₁,A₂,A₃... are located of equal distances on the ray AX and the points P is joined to

To draw a pair of tangents to a circle which are inclined to each other at an angle of 35°, it is required to draw tangents at the end points of those two radii of the circle, the angle between which is :

To draw a pair of tangents to circle which are inclined to each other at angle of 60°, it is required to draw tangents at end points of those two radii of the circle, the angle between them should be :

A draw a pair of tangents to a circle which are inclined to each other at an angle of 65°, it is required to draw tangents at the end points of those two radii of the circle, the angle between which is :

To draw a pair tangents to a circle which are inclined to each other at an angle of 70°, it is required to draw tangents at end points of those two radii of the circle, the angle between them should be 

If two tangents are drawn at the end points of two radii of a circle which are inclined at 120° to each other, then the pair of tangents will be inclined to each other at an angle of

To draw a pair of tangents to a circle which are at right angles to each other, it is required to draw tangents at end points of the two radii of the circle, which are inclined at an angle of

To draw a pair of tangents to a circle which are inclined to each other at an angle of 45° it is required to draw tangents at the end points of the two radii of the circle, which are inclined at an angle of

To draw a pair of tangents to a circle which are inclined to each other at angle x°, it is required to draw tangents at the end points of those two radii of the circle, the angle between which is

To draw tangents to each of the circle with radii 3 cm and 2 cm from the centre of the other circle, such that the distance between their centres A and B is 6 cm, a perpendicular bisector of AB is drawn intersecting AB at M. The next step is to draw

To draw tangents to a circle of radius ‘p’ from a point on the concentric circle of radius ‘q’, the first step is to find

To draw a tangent at point B to the circumcircle of an isosceles right ΔABCright angled at B, we need to draw through B

A pair of tangents can be constructed to a circle inclined at an angle of :

A pair of tangents can be constructed to a circle from an external point, which are inclined each other at an angle θ such that :

Two distinct tangents can be constructed from a point P to a circle of radius 2r situated at a distance:

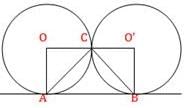
Two circles touch each other externally at C and AB is a common tangent to the circles. Then, ∠ACB =