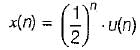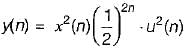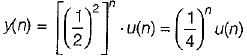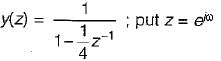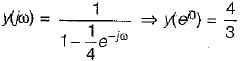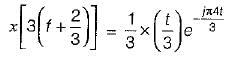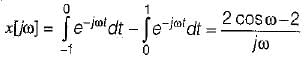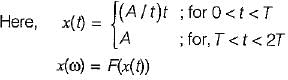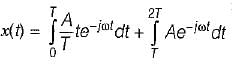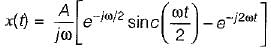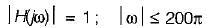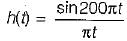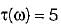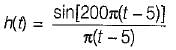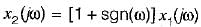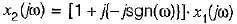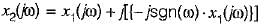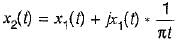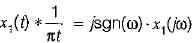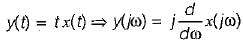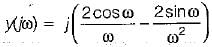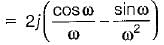Test: Continuous Time Fourier Transformer (CTFT)- 2 - Electronics and Communication Engineering (ECE) MCQ
10 Questions MCQ Test - Test: Continuous Time Fourier Transformer (CTFT)- 2
If x(n) = (1/2)n u(n), y(n) = x2(n) and (eiω) be the fourier transform of y(n), then y(e0) is
For a signal x(t), the fourier transform is X(f), then inverse fourier transform of x(3f + 2) is given by
The Fourier transform of given signal x(t)

Fourier transform of x(t) = eat u (-t), a > 0 is
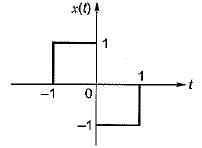
Determine the fourier transform of the signal x(t) shown in figure.
Match List-I [Function f(t)] with List-II [Fourier transform F(ω)] and select the correct answer using the codes given below the lists:
List- I
A. f(t – t0)
B. f(t) ejω0t
C. f1(t) . f2(t)
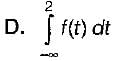
List-ll
1. f(ω – ω0)
2.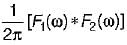
3. 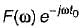
4.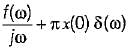
5.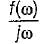
Codes
Consider a continuous time low pass filter whose impulse response h(t) is known to be real and whouse frequency response magnitude is given by
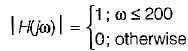
Determine the value of h(t) if the group delay function is specified as t(ω) = 5.
Consider a signal x1(t) having a fourier transform x1(jω). An another signal x2(t) having fourier transform x2(jω) is related to x1 (t) by x2(jω) = [1 +sgn(ω)] x1(jω) x2(t) in terms of x1(t) is equal to
A Fourier transform pair is as follows:
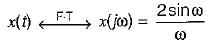
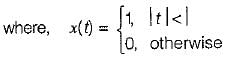
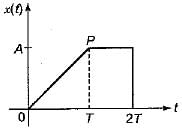
The Fourier transform of given signal y(t) is
Suppose; y(t) = x(t) cost
and 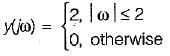
then x(t) will be