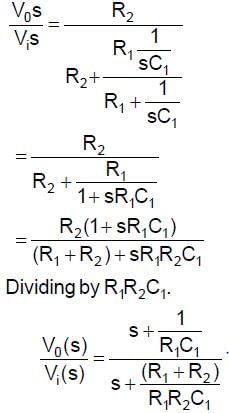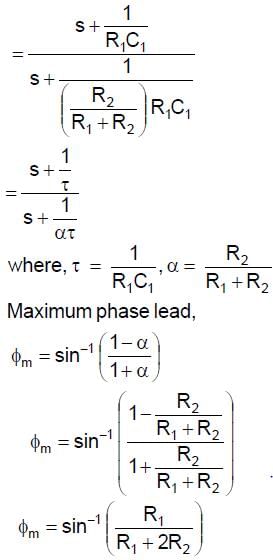Test: Control System - 1 - Electronics and Communication Engineering (ECE) MCQ

A control system has input r(t) and output c(t). If the input is first passed through a block

whose transfer function is a^-2s and then applied to the system, the modified output will be

The open-loop transfer function of a feedback control system is given by G(s)

Find the range of the values of T for stability.

If the open-loop transfer function of a feedback system is given by

G(s) H(s) = , then the controid of the asymptotes will be

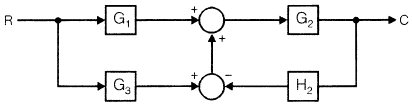
For the block diagram shown in figure below, the limiting value of k for stability of the inner loop is found to be X < k < Y. The overall system will be stable if and only if

The closed loop transfer function of a control system has the following poles and zeros

Poles                                                       Zeros

P₁ =    0.5                                                          Z₁ = –7

P₂ = –1.0                                                          Z₂ = 9

P₃ = –5

P₄ = —10

The closed loop response can be closely approximated by considering which of the following?

Match List-I (Type of compensator) with List-II (Polar plot) and select the correct answer using the code given below the lists:

List-I   

1.Phase lead                                   

2. Phase lag                                   

3. Lead-lag                                       

    A B C

(a)123

(b) 132

(c) 213

(d) 231

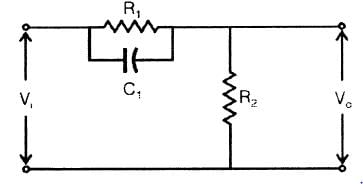
For the given network, the maximum phase lead _4m of V_o with respect to V₁ is

In the Bode-plot of a unity feedback control system, the value of phase of G(j@) at the gain

cross-over frequency is —125°. The phase margin of the system is

The Nyquist plot for the function is

The condition for stability is given by

The open-loop transfer function of unity feedback system is G(s) =  . Thes (s + 2) (s + 10)range of k for which closed-loop system is stable.

The Bode plot for minimum phase transfer function is:

For the system shown below the state-space equation is X = A x + B u. The matrix A is