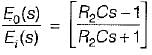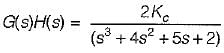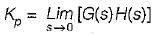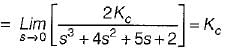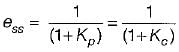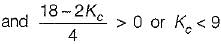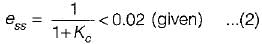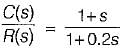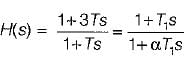Test: Controllers & Compensators - 2
20 Questions MCQ Test GATE Electrical Engineering (EE) 2023 Mock Test Series | Test: Controllers & Compensators - 2
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
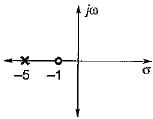
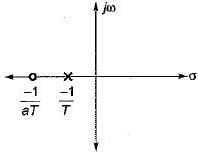
Assertion (A) : The phase lag network provides an attenuation of 20 log a (a < 1) at high frequencies having transfer function equal to
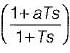
Reason (R): The lag network allows to pass high frequencies and low frequencies are attenuated.
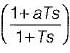
Reason (R): The lag network allows to pass high frequencies and low frequencies are attenuated.
Here, reason (R) is false because the lag network allows to pass low frequencies and high frequencies are attenuated.
Assertion (A): Introduction of phase lag network in forward path increases the phase shift.
Reason (R): A phase lag network has pole nearer to the imaginary axis as compared to zero.
Reason (R): A phase lag network has pole nearer to the imaginary axis as compared to zero.
The transfer function of a phase-lag network is:
The pole-zero plot is shown below:
Here, pole is nearer to the imaginary axis and origin compared to zero.
Hence, reason (R) is true.
Introduction of phase lag network in forward path reduces the phase shift. Hence, assertion (A) is a false statement.
Match List-I (Type of controllers) with List-ll (Alternate names) and select the correct answer using the codes given below the lists:
List-I
A. Two-position controller
B. Proportional controller
C. Integral controller
D. Derivative controller
List-II
1. Rate controller
2. Reset controller
3. An amplifier with adjustable gain
4. ON-OFF controller
Codes:
A B C D
(a) 4 2 3 1
(b) 4 3 2 1
(c) 3 4 2 1
(d) 3 4 1 2
List-I
A. Two-position controller
B. Proportional controller
C. Integral controller
D. Derivative controller
List-II
1. Rate controller
2. Reset controller
3. An amplifier with adjustable gain
4. ON-OFF controller
Codes:
A B C D
(a) 4 2 3 1
(b) 4 3 2 1
(c) 3 4 2 1
(d) 3 4 1 2
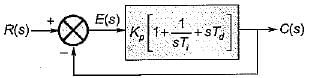
The open loop transfer function of a three action controller (PID controller) is given by
A PID controller is shown below.
Here,
G(s) = O.L.T.F
Due to PD controller, a zero is added to the forward path which results in a lead compensator. Therefore, steady state error remais the same whiie rise time of the system is reduced (i.e. stability is increased).
For the derivative feedback control shown in figure below, the damping ratio is equal to 0.7
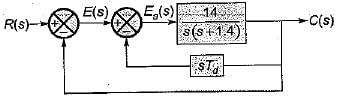
The value of derivative gain constant is
For the given system, characteristic equation is
or,
s2 + 1.4s + 14s Td + 14 = 0
or,
s2 + (1.4 + 14Td) s + 14 = 0
Comparing with s2 + 2 ξωn + ωn2 =0, we have:
ωn = √14 rad/s and 2ξωn = (1.4 + 14Td)
or, 2 x 0.7 x √14 = 1.4 + 14 Td (∴ ξ = 0.7, given)
or,
or,
= 0.274
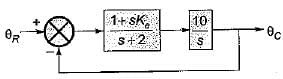
The block diagram of an integral control is shown in figure below.
The steady state error in the above system for a parabolic input is
For the given system, forward path transfer function is
For parabolic input, steady state error is
where,
∴ 
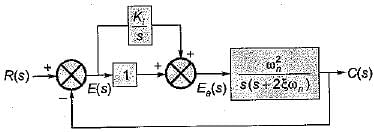
A system employing proportional plus error rate control is shown in figure below.
The value of error rate control (Ke) and 2% settling time for a damping ratio of 0.5 are respectively
The forward path gain of the given system is:
∴ Characteristic equation is
1 + G(s)H(s) = 0
or
or, s2 + (2 + 10 Ke)s +10 = 0
Here,
ωn = √10 rad/s
and 2ξωn = (2 + 10Ke)
Given, ξ = 0.5
So, 2 x 0.5 x √10 = (2 + 10Ke)
or,
= 1.16/10 = 0.116
Also, 2% settling time
A feedback control system employing output- rate damping is shown in figure below.
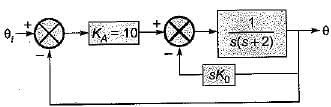
What is the steady state error (in radian) for the above system resulting from an unit ramp input if the damping ratio is 0.6?
The characteristic equation of the given system is
1+G(s) H(s) = 0
Here,
∴ Characteristic equation is
10
or, s2 + (K0 + 2)s +10 = 0
Comparing with s2 + 2ξωns + ωn2 = 0 we have
ωn = √10 rad/s
and 2ξωn = K0 + 2
Given, ξ = 0.6
∴ 2 x 0.6 x √10 = K0 + 2
or, K0 = 1.792
For a unit ramp input, ess = 1/Kv
where,
∴ 
= 0.3792 ≈ 0.38 radian
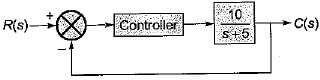
In the control system shown below, the controller which can give infinite value of steady-stae error to a ramp input is
Case-1: For integral type
∴ 
∴ ess = Ti/2
Case-2: For derivative type
G(s)H(s) = (10sTd)/(s+5)
∴ 
∴ ess = 1/Kv = ∞
Case-3: For proportional type
G(s)H(s) = 10Kp/(s+5)
∴ 
∴ 
Case-4: For proportional plus derivative type
∴ 
∴ ess = 1/Kv = ∞
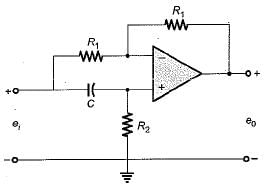
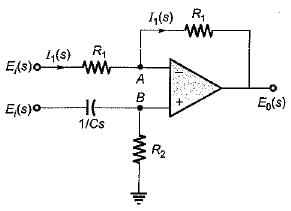
The transfer function of the OP-AMP circuit shown below is given by:
Redrawing the given circuit in s-domain, we have:
Now,
From virtual ground concept,
Now,
or,
2VA(s) = Ei(s) + E0(s)
E0(s) = 2VA(s) - Ei(s)
or,
or,
The transfer function of a phase lead compensator is given by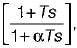 
where α < 1 and T> 0.
Which of the following is not a correct value of maximum phase shift provided by such a compensator?
Assertion (A): Stepping motors are compatible with modern digital systems.
Reason (R): The nature of command is in the forms of pulses.
Since the nature of command is in the form of pulses, therefore stepping motors are compatible with modern digital systems.
Consider the control system shown in figure below employing a proportional compensator.
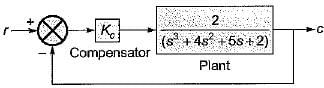
If the steady-state error has to be less than two percent for a unit step input, then the value of Kc would be
For given system,
With proportional controller,
∴ 
(for a unit step input)
Given, ess = less than 2% of input
i.e. ess < 0.02
Now, characteristic equation is:
1 + G(s)H(s) = 0
or, s3 + 4s2 + 5s + 2 + 2Kc = 0
Routh’s array is:
For stability of given system,
2 + 2Kc > 0 or Kc > -1
or Kc < 9
Hence, -1 < Kc < 9 (for stability) ....... (1)
Now,
From equations (1) and (2), we conclude that the minimum value of steady state error = 0.1 when Kc = 9.
Also, for all value of Kc between -1 and 9, value of ess will be more than 0.02 i.e. more than 2% of input.
Therefore, there is no such value of Kc for given system i.e. can not be determined.
Match List-I (Controllers) with List-II (Transfer functions) and select the correct answer using the codes given below the lists:
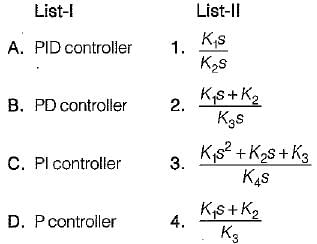
Codes:
A B C D
(a) 2 3 4 1
(b) 3 4 1 2
(c) 3 4 2 1
(d) 3 1 4 2
The transfer function of a system is given as:
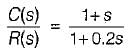
It represents a
Given,
The pole-zero plot is shown below.
Since zero is near to origin, therefore it represents a lead network.
The industrial controller having the best steady state accuracy is
The transfer function of a phase lead controller is
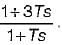
The maximum value of phase shift provided by this controller is
Given,
Here, T1 = 3T and αT1 = T
∴ α = T/T1 = T/3T = 1/3
∴
or, ϕm = 30° = maximum phase shift
With regard to the filtering property, the lead compensator and the lag compensators are respectively
|
22 docs|274 tests
|
|
22 docs|274 tests
|
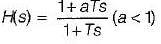
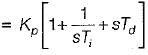
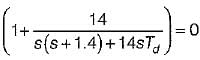
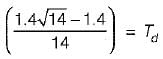
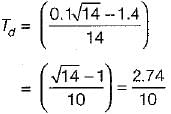
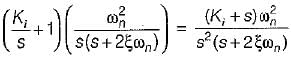
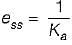
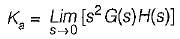
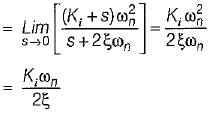
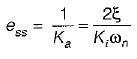
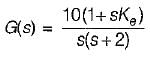
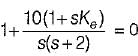
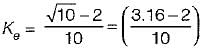
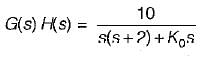
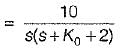
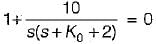
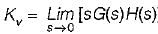
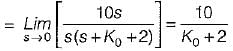
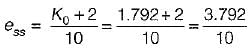
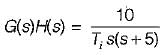
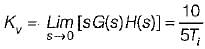
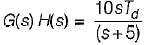
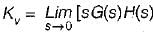
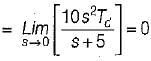
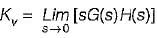
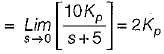
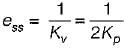
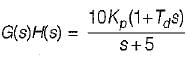
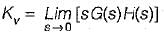
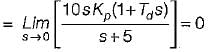
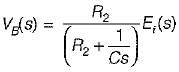
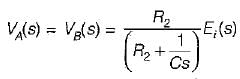
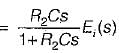
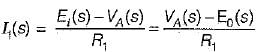
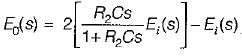Top Courses for Electronics and Communication Engineering (ECE)
Download free EduRev App
(Scan QR code)
|
|
|
© EduRev
|
Education Revolution
|
Follow Us
|
