Test: Coordinate Geometry- 1 - GMAT MCQ
15 Questions MCQ Test Quantitative for GMAT - Test: Coordinate Geometry- 1
If the x-intercept of line L is -5 and the slope is equal to 5/2, Find the y-intercept of the line L.
Which of the following line is parallel to the given line 3x + 4y = 12 and has a negative y-intercept.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
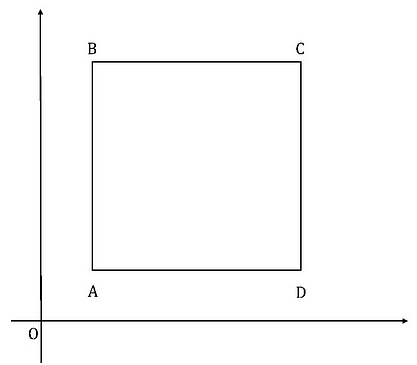
In the given diagram, ABCD is a square and the coordinate of B is (5,5). If the length of each side is 2 units and AB is parallel to the y-axis, find the coordinate of D.
In the given diagram, the circle touches the y-axis at the point K whose coordinate is (0,7). If the area of triangle CKO is 21 units2, where C is the centre of the circle, find the area of the circle.
The graph of the equation x2y = k, where k < 0, lies in which two quadrants shown above?
Lines a and b, not shown, lie in the rectangular coordinate system shown above. Is the slope of line a greater than the slope of line b?
(1) Line a does not intersect quadrant III.
(2) Line b intersects quadrant IV.
A circle is tangent to the x-axis at 2 and the y-axis at 2. What is the area of the region between the circle and the origin?
If L1 passes through points in each quadrant except the IIIrd quadrant, then is the slope of the line L2 positive?
(1) L2 is perpendicular to L1.
(2) L1 and L2 intersect in the Ist quadrant.
On the x-y coordinate grid, if points P, Q, and R make a triangle (not shown), what is the area of the triangle?
(1) Point Q lies on the x-axis 6 units from point P.
(2) Point R is 5 units away from the x-axis
On the x-y coordinate grid, are points A and B equidistant from the origin?
(1) |x| = |y| for point A and |x| = |y| for point B
(2) |x|, |y| of point A = |x|, |y| of point B
In which quadrant does the point (x,y) lie?
(1) (x, y+1) lies in the IInd Quadrant.
(2) (x + 3, y) lies in the IIIrd Quadrant.
In the xy-plane, the line y = k is the perpendicular bisector of the line segment PQ and the line x = h is the perpendicular bisector of the line segment RQ. If the coordinates of the point R are (-h, -k), then what are the coordinates of the point P?
On the x-y coordinate grid, does the line passing through point P (not shown) have a slope greater than 2?
(1) Point P has an x-value of 1 and is 2 units away from the origin
(2) The line does not pass through Quadrant IV
In the rectangular coordinate system above, if OB < BC then is the area of the triangle ABC lesser than 12 square units?
(1) Point A lies above the line y = 5
(2) The mid-point of B and C is (6, 0)
In the xy-plane, is the x-intercept of the line y = mx + b positive? (m and b are non-zero numbers)
(1) The y-intercept of the line m2y = bx + m is positive.
(2) The x-intercept of the line is positive
|
115 videos|106 docs|113 tests
|
|
115 videos|106 docs|113 tests
|

















