CAT Exam > CAT Tests > Quantitative Aptitude (Quant) > Test: Coordinate Geometry- 1 - CAT MCQ
Test: Coordinate Geometry- 1 - CAT MCQ
Test Description
10 Questions MCQ Test Quantitative Aptitude (Quant) - Test: Coordinate Geometry- 1
Test: Coordinate Geometry- 1 for CAT 2024 is part of Quantitative Aptitude (Quant) preparation. The Test: Coordinate Geometry- 1 questions and answers have been
prepared according to the CAT exam syllabus.The Test: Coordinate Geometry- 1 MCQs are made for CAT 2024 Exam. Find important
definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Test: Coordinate Geometry- 1 below.
Solutions of Test: Coordinate Geometry- 1 questions in English are available as part of our Quantitative Aptitude (Quant) for CAT & Test: Coordinate Geometry- 1 solutions in
Hindi for Quantitative Aptitude (Quant) course. Download more important topics, notes, lectures and mock
test series for CAT Exam by signing up for free. Attempt Test: Coordinate Geometry- 1 | 10 questions in 10 minutes | Mock test for CAT preparation | Free important questions MCQ to study Quantitative Aptitude (Quant) for CAT Exam | Download free PDF with solutions
Test: Coordinate Geometry- 1 - Question 1
Q.
We divided the plane of the paper into four equal parts. by drawing two mutually perpendicular lines, X'OX and YOY'. These lines are called the axes. Here X'OX is called x-axis and YOY' is called y-axis. There axes divide the plane of the paper into four parts, called quadrants.
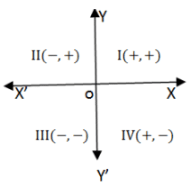
The position of a point in a plane is denoted by an ordered pair (a,b), where a is called the x co-ordinate and y is called y co-ordinate.
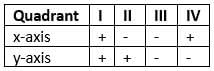
In which quadrant does the point(-4, -7) lie?
Detailed Solution for Test: Coordinate Geometry- 1 - Question 1
Detailed Solution for Test: Coordinate Geometry- 1 - Question 2
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Detailed Solution for Test: Coordinate Geometry- 1 - Question 3
Detailed Solution for Test: Coordinate Geometry- 1 - Question 4
Detailed Solution for Test: Coordinate Geometry- 1 - Question 5
Test: Coordinate Geometry- 1 - Question 6
Find the distance of the point A(3, -3) from the origin.
Detailed Solution for Test: Coordinate Geometry- 1 - Question 6
Test: Coordinate Geometry- 1 - Question 7
P is a point on x-axis at a distance of 4 units from y-axis to its right. The co-ordinates of P are:
Detailed Solution for Test: Coordinate Geometry- 1 - Question 7
Test: Coordinate Geometry- 1 - Question 8
The area of the triangle whose vertices are (a,a), (a + 1, a + 1) and (a + 2, a) is
Detailed Solution for Test: Coordinate Geometry- 1 - Question 8
Test: Coordinate Geometry- 1 - Question 9
A is a point on y-axis at a distance of 5 units from x-axis lying below x-axis. The co-ordinates of A are:
Detailed Solution for Test: Coordinate Geometry- 1 - Question 9
Test: Coordinate Geometry- 1 - Question 10
ABCD is a rhombus with the diagonals AC and BD intersection at the origin on the x-y plane. The equation of the straight line AD is x + y = 1. What is the equation of BC?
Detailed Solution for Test: Coordinate Geometry- 1 - Question 10
|
191 videos|131 docs|110 tests
|
Information about Test: Coordinate Geometry- 1 Page
In this test you can find the Exam questions for Test: Coordinate Geometry- 1 solved & explained in the simplest way possible.
Besides giving Questions and answers for Test: Coordinate Geometry- 1, EduRev gives you an ample number of Online tests for practice
|
191 videos|131 docs|110 tests
|
Download as PDF
Top Courses for CAT
Important Questions for Coordinate Geometry- 1
Find all the important questions for Coordinate Geometry- 1 at EduRev.Get fully prepared for Coordinate Geometry- 1 with EduRev's comprehensive question bank and test resources.
Our platform offers a diverse range of question papers covering various topics within the Coordinate Geometry- 1 syllabus.
Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered.
The questions are designed to challenge you and help you gain confidence in tackling the actual exam.
Maximize your chances of success by utilizing EduRev's extensive collection of Coordinate Geometry- 1 resources.
Coordinate Geometry- 1 MCQs with Answers
Prepare for the Coordinate Geometry- 1 within the CAT exam with comprehensive MCQs and answers at EduRev.
Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus.
Access the best books, study materials, and notes curated by toppers to enhance your preparation.
Stay updated with the exam date and receive expert preparation tips and paper analysis.
Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.
Online Tests for Coordinate Geometry- 1 Quantitative Aptitude (Quant)
Practice with a wide array of question papers that follow the exam pattern and syllabus.
Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement.
Access detailed solutions and explanations for each test to enhance your understanding of concepts.
With EduRev's Online Tests, you can build confidence, boost your performance, and ace Coordinate Geometry- 1 with ease.
Join thousands of successful students who have benefited from our trusted online resources.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup