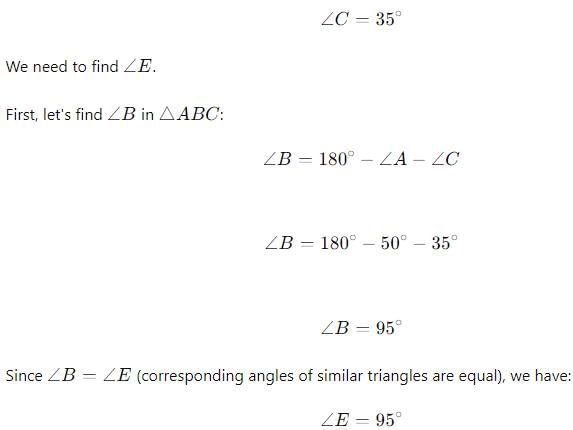Test: Criteria for Similar Triangles - Grade 10 MCQ
10 Questions MCQ Test - Test: Criteria for Similar Triangles
If ΔDEF ~ ΔABC and DE = AB, what is the relation between the two triangles?
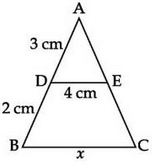
In the following figure, find the value of x.
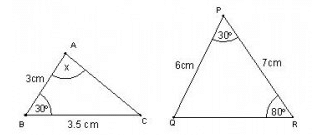
In the figure given below, if DE || BC, then x equals :
Given that ΔABC ~ ΔDEF and AB = 2cm , BC = 3cm, DE = 4cm, EF = 6cm , If DF = 8cm, then AC = ?
If ΔPQR ~ ΔXYZ, ∠Q = 50°, ∠R = 70° then ∠X is equal to :
Given that ΔABC ~ ΔDEF ∠A = 50°, ∠C = 35° ∠E = ?
In the given figure perpendiculars are dropped on the common base BD of the given two triangles. AE = 2cm, CF = 3cm
In the given figure ΔABC ~ ΔBDC = 90° each. Choose the correct similarity from the given choices.
ΔABC ~ ΔDEF Perimeter (ΔABC) = 15 cm, Perimeter (DEF) = 25 cm.If AB = 6 cm, then find DE.
In the given figure use the similarity of the given triangles to find the value of BD,
ΔABC ~ ΔBDC, ∠BDC = ∠ABC = 90°, AB = 3, BC = 4,AD = 2, BD = ?



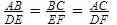
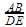 =2/4=½
=2/4=½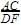 =½
=½