Test: Cubes & Cuboids
31 Questions MCQ Test Logical Reasoning (LR) and Data Interpretation (DI) | Test: Cubes & Cuboids
| 1 Crore+ students have signed up on EduRev. Have you? |
Directions to Solve
The following questions are based on the information given below:
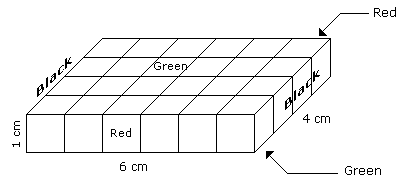
- A cuboid shaped wooden block has 6 cm length, 4 cm breadth and 1 cm height.
- Two faces measuring 4 cm x 1 cm are coloured in black.
- Two faces measuring 6 cm x 1 cm are coloured in red.
- Two faces measuring 6 cm x 4 cm are coloured in green.
- The block is divided into 6 equal cubes of side 1 cm (from 6 cm side), 4 equal cubes of side 1 cm(from 4 cm side).
Question -
How many cubes having red, green and black colours on at least one side of the cube will be formed ?
Such cubes are related to the corners of the cuboid. Since the number of corners of the cuboid is 4.
Hence, the number of such small cubes is 4.
Directions to Solve
The following questions are based on the information given below:
All the opposite faces of a big cube are coloured with red, black and green colours. After that is cut into 64 small equal cubes.
Question -
How many small cubes are there where one face is green and other one is either black or red ?
Number of small cubes having one face green and the other one is either red or black = 8 x 2 = 16
Directions to Solve
The following questions are based on the information given below:
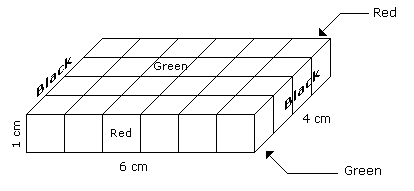
- A cuboid shaped wooden block has 6 cm length, 4 cm breadth and 1 cm height.
- Two faces measuring 4 cm x 1 cm are coloured in black.
- Two faces measuring 6 cm x 1 cm are coloured in red.
- Two faces measuring 6 cm x 4 cm are coloured in green.
- The block is divided into 6 equal cubes of side 1 cm (from 6 cm side), 4 equal cubes of side 1 cm(from 4 cm side).
Question -
How many small cubes will be formed ?
Number of small cubes = l x b x h = 6 x 4 x 1 = 24
Directions to Solve
The following questions are based on the information given below:
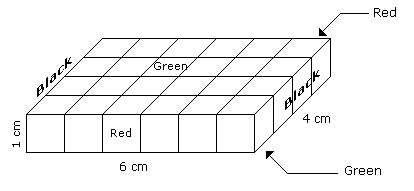
- A cuboid shaped wooden block has 6 cm length, 4 cm breadth and 1 cm height.
- Two faces measuring 4 cm x 1 cm are coloured in black.
- Two faces measuring 6 cm x 1 cm are coloured in red.
- Two faces measuring 6 cm x 4 cm are coloured in green.
- The block is divided into 6 equal cubes of side 1 cm (from 6 cm side), 4 equal cubes of side 1 cm(from 4 cm side).
Question -
How many cubes will have 4 coloured sides and two non-coloured sides ?
Only 4 cubes situated at the corners of the cuboid will have 4 coloured and 2 non-coloured sides.
Directions to Solve
The following questions are based on the information given below:
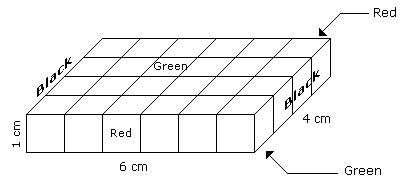
- A cuboid shaped wooden block has 6 cm length, 4 cm breadth and 1 cm height.
- Two faces measuring 4 cm x 1 cm are coloured in black.
- Two faces measuring 6 cm x 1 cm are coloured in red.
- Two faces measuring 6 cm x 4 cm are coloured in green.
- The block is divided into 6 equal cubes of side 1 cm (from 6 cm side), 4 equal cubes of side 1 cm(from 4 cm side).
Question -
How many cubes will remain if the cubes having black and green coloured are removed ?
Number of small cubes which are Black and Green is 8 in all.
Hence, the number of remaining cubes are = 24 - 8 = 16
Directions to Solve
The following questions are based on the information given below:
- A cuboid shaped wooden block has 6 cm length, 4 cm breadth and 1 cm height.
- Two faces measuring 4 cm x 1 cm are coloured in black.
- Two faces measuring 6 cm x 1 cm are coloured in red.
- Two faces measuring 6 cm x 4 cm are coloured in green.
- The block is divided into 6 equal cubes of side 1 cm (from 6 cm side), 4 equal cubes of side 1 cm(from 4 cm side).
Question -
How many cubes will have green colour on two sides and rest of the four sides having no colour ?
There are 16 small cubes attached to the outer walls of the cuboid.
Therefore remaining inner small cubes will be the cubes having two sides green coloured.
So the required number = 24 - 16 = 8
Directions to Solve
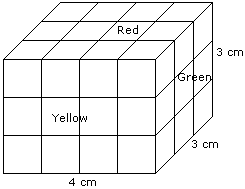
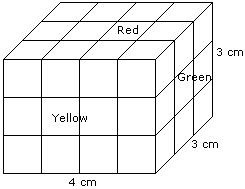
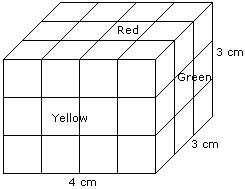
The following questions are based on the information given below:
- There is a cuboid whose dimensions are 4 x 3 x 3 cm.
- The opposite faces of dimensions 4 x 3 are coloured yellow.
- The opposite faces of other dimensions 4 x 3 are coloured red.
- The opposite faces of dimensions 3 x 3 are coloured green.
- Now the cuboid is cut into small cubes of side 1 cm.
Question -
How many small cubes will have only two faces coloured ?
Number of small cubes having only two faces coloured = 6 from the front + 6 from the back + 2 from the left + 2 from the right
= 16
Directions to Solve
The following questions are based on the information given below:
- There is a cuboid whose dimensions are 4 x 3 x 3 cm.
- The opposite faces of dimensions 4 x 3 are coloured yellow.
- The opposite faces of other dimensions 4 x 3 are coloured red.
- The opposite faces of dimensions 3 x 3 are coloured green.
- Now the cuboid is cut into small cubes of side 1 cm.
Question -
How many small cubes have three faces coloured ?
Such cubes are related to the corners of the cuboid and there are 8 corners.
Hence, the required number is 8.
Directions to Solve
The following questions are based on the information given below:
- There is a cuboid whose dimensions are 4 x 3 x 3 cm.
- The opposite faces of dimensions 4 x 3 are coloured yellow.
- The opposite faces of other dimensions 4 x 3 are coloured red.
- The opposite faces of dimensions 3 x 3 are coloured green.
- Now the cuboid is cut into small cubes of side 1 cm.
Question -
How many small cubes will have no face coloured ?
Number of small cubes have no face coloured = (4 - 2) x (3 - 2) = 2 x 1 = 2
Directions to Solve
The following questions are based on the information given below:
- There is a cuboid whose dimensions are 4 x 3 x 3 cm.
- The opposite faces of dimensions 4 x 3 are coloured yellow.
- The opposite faces of other dimensions 4 x 3 are coloured red.
- The opposite faces of dimensions 3 x 3 are coloured green.
- Now the cuboid is cut into small cubes of side 1 cm.
Question -
How many small cubes will have only one face coloured ?
Number of small cubes having only one face coloured = 2 x 2 + 2 x 2 + 2 x 1
= 4 + 4 + 2
= 10
Directions to Solve
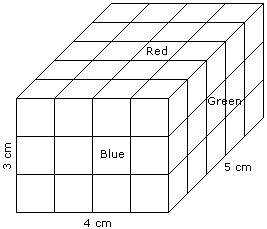
The following questions are based on the information given below:
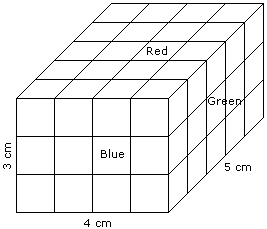
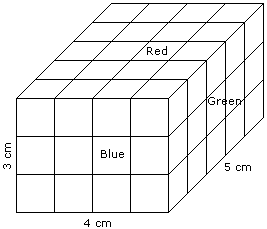
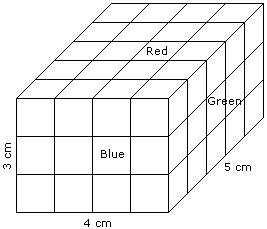
- A cuboid shaped wooden block has 4 cm length, 3 cm breadth and 5 cm height.
- Two sides measuring 5 cm x 4 cm are coloured in red.
- Two faces measuring 4 cm x 3 cm are coloured in blue.
- Two faces measuring 5 cm x 3 cm are coloured in green.
- Now the block is divided into small cubes of side 1 cm each.
Question -
How many small cubes will have will have three faces coloured ?
Such cubes are related to the corners of the cuboid and in the cuboid there are 8 corners.
Hence, the required number of small cubes is 8.
Directions to Solve
The following questions are based on the information given below:
- A cuboid shaped wooden block has 4 cm length, 3 cm breadth and 5 cm height.
- Two sides measuring 5 cm x 4 cm are coloured in red.
- Two faces measuring 4 cm x 3 cm are coloured in blue.
- Two faces measuring 5 cm x 3 cm are coloured in green.
- Now the block is divided into small cubes of side 1 cm each.
Question -
How many small cubes will have only one face coloured ?
2 from the front + 2 from the back + 3 from the left + 3 from the right + 6 from the top + 6 from the bottom = 22
Directions to Solve
The following questions are based on the information given below:
- A cuboid shaped wooden block has 4 cm length, 3 cm breadth and 5 cm height.
- Two sides measuring 5 cm x 4 cm are coloured in red.
- Two faces measuring 4 cm x 3 cm are coloured in blue.
- Two faces measuring 5 cm x 3 cm are coloured in green.
- Now the block is divided into small cubes of side 1 cm each.
Question -
How many small cubes will have no faces coloured ?
Required number of small cubes = (5 - 2) x (4 - 2) x (3 - 2)
= 3 x 2 x 1
= 6
Directions to Solve
The following questions are based on the information given below:
- A cuboid shaped wooden block has 4 cm length, 3 cm breadth and 5 cm height.
- Two sides measuring 5 cm x 4 cm are coloured in red.
- Two faces measuring 4 cm x 3 cm are coloured in blue.
- Two faces measuring 5 cm x 3 cm are coloured in green.
- Now the block is divided into small cubes of side 1 cm each.
Question -
How many small cubes will have two faces coloured with red and green colours ?
Required number of small cubes = 6 from the top and 6 from the bottom = 12
Directions to Solve
The following questions are based on the information given below:
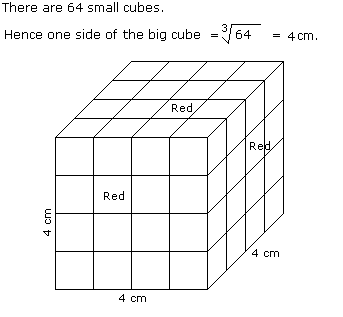
- All the faces of cubes are painted with red colour.
- The cubes is cut into 64 equal small cubes.
Question -
How many small cubes have only one face coloured ?
Number of small cubes having only one face coloured = (x - 2)2 x No. of faces
= (4 - 2)2 x 6
= 24
Directions to Solve
The following questions are based on the information given below:
- All the faces of cubes are painted with red colour.
- The cubes is cut into 64 equal small cubes.
Question -
How many small cubes have no faces coloured ?
Number of small cubes having only one faces coloured = (x - 2)3
Here, x = side of big cube / side of small cube
x = 4 /1
x = 4
Required number = (4 -2)3
= 8
Directions to Solve
The following questions are based on the information given below:
- All the faces of cubes are painted with red colour.
- The cubes is cut into 64 equal small cubes.
Question -
How many small cubes are there whose three faces are coloured ?
Number of small cubes having three faces coloured = No. of corners = 8
Directions to Solve
The following questions are based on the information given below:
- All the faces of cubes are painted with red colour.
- The cubes is cut into 64 equal small cubes.
Question -
How many small cubes are there whose two adjacent faces are coloured red ?
Number of small cubes having two adjacent faces coloured red = (x - 2) x No. of edges
= (4 - 2) x 12
= 24
Directions to Solve
The following questions are based on the information given below:
All the opposite faces of a big cube are coloured with red, black and green colours. After that is cut into 64 small equal cubes.
Question -
How many small cubes are there whose no faces are coloured ?
Number of small cubes having no face coloured = (x - 2)3
= (4 - 2)3
= 8
Directions to Solve
The following questions are based on the information given below:
All the opposite faces of a big cube are coloured with red, black and green colours. After that is cut into 64 small equal cubes.
Question -
How many small cubes are there whose 3 faces are coloured ?
Number of small cubes having three faces coloured = 1 at each corner
= 1 x 8
= 8
>
Directions to Solve
The following questions are based on the information given below:
All the opposite faces of a big cube are coloured with red, black and green colours. After that is cut into 64 small equal cubes.
Question -
How many small cubes are there whose only one face is coloured ?
Number of small cubes having only one face coloured = 4 from each face
= 4 x 6
= 24
Directions to Solve
The following questions are based on the information given below:
All the opposite faces of a big cube are coloured with red, black and green colours. After that is cut into 64 small equal cubes.
Question -
How many small cubes are there whose at the most two faces are coloured ?
Number of small cubes having two faces coloured = 8 + 8 + 4 + 4 = 24
and Number of small cubes having only one face coloured = 4 x 6 = 24
and Number of small cubes having no face coloured = 4 + 4 = 8
Therefore, total number of small cubes whose at the most two faces are coloured = 24 + 24 + 8 = 56.
Directions to Solve
All the faces of a cube are painted with blue colour. Then it is cut into 125 small equal cubes.
Question -
How many small cubes will be formed having only one face coloured ?
No. of small cubes having only one face coloured = (5 - 2)2 x 6
= 9 x 6
= 54
Directions to Solve
All the faces of a cube are painted with blue colour. Then it is cut into 125 small equal cubes.
Question -
How many small cubes will be formed having no face coloured ?
No. of small cubes having no face coloured = (x - 2)3
= (5 - 2)3
= 27
Directions to Solve
All the six faces of a cube of a cube are coloured with six different colours - black, brown, green, red, white and blue.
- Red face is opposite to the black face.
- Green face is between red and black faces.
- Blue face is adjacent to white face.
- Brown face is adjacent to blue face.
- Red face is in the bottom.
Question -
The upper face is _________
Directions to Solve
All the six faces of a cube of a cube are coloured with six different colours - black, brown, green, red, white and blue.
- Red face is opposite to the black face.
- Green face is between red and black faces.
- Blue face is adjacent to white face.
- Brown face is adjacent to blue face.
- Red face is in the bottom.
Question -
Which of the following is adjacent to green ?
Directions to Solve
All the six faces of a cube of a cube are coloured with six different colours - black, brown, green, red, white and blue.
- Red face is opposite to the black face.
- Green face is between red and black faces.
- Blue face is adjacent to white face.
- Brown face is adjacent to blue face.
- Red face is in the bottom.
Question -
Which face is opposite to green ?
Directions to Solve
There are 128 cubes with me which are coloured according to two schemes viz.
- 64 cubes each having two red adjacent faces and one yellow and other blue on their opposite faces while green on the rest.
- 64 cubes each having two adjacent blue faces and one red and other green on their opposite faces, while red on the rest. They are then mixed up.
Question -
How many cubes have at least two coloured red faces each ?
64 and 64 cubes of both types of cubes are such who have at least two coloured faces red each.
Therefore, total number of the required cubes is 128.
Directions to Solve
There are 128 cubes with me which are coloured according to two schemes viz.
- 64 cubes each having two red adjacent faces and one yellow and other blue on their opposite faces while green on the rest.
- 64 cubes each having two adjacent blue faces and one red and other green on their opposite faces, while red on the rest. They are then mixed up.
Question -
What is the total number of red faces ?
No. of red faces among first 64 cubes = 128
No. of red faces among second 64 cubes = 192
Therefore, total number of red faces = 128 + 192 = 320
Directions to Solve
There are 128 cubes with me which are coloured according to two schemes viz.
- 64 cubes each having two red adjacent faces and one yellow and other blue on their opposite faces while green on the rest.
- 64 cubes each having two adjacent blue faces and one red and other green on their opposite faces, while red on the rest. They are then mixed up.
Question -
Which two colours have the same number of faces ?
First 64 cubes are such each of whose two faces are green and second 64 cubes are such each of whose two faces are blue.
Therefore, green and blue colours have the same number of faces.
Directions to Solve
There are 128 cubes with me which are coloured according to two schemes viz.
- 64 cubes each having two red adjacent faces and one yellow and other blue on their opposite faces while green on the rest.
- 64 cubes each having two adjacent blue faces and one red and other green on their opposite faces, while red on the rest. They are then mixed up.
Question -
How many cubes have two adjacent blue faces each ?
Second 64 cubes are such each of whose two faces are blue.
|
96 videos|90 docs|119 tests
|
|
Use Code STAYHOME200 and get INR 200 additional OFF
|
Use Coupon Code |
|
96 videos|90 docs|119 tests
|
How to Prepare for CAT
Download free EduRev App
Related content with Test: Cubes & Cuboids
|
|
|
|
Related tests with Test: Cubes & Cuboids
|
|
|
|
|
|
© EduRev
|
Education Revolution
|
Follow Us
|
