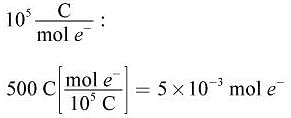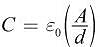Test: Current and Resistance - MCAT MCQ
10 Questions MCQ Test Physics for MCAT - Test: Current and Resistance
If a defibrillator passes 15 A of current through a patient's body for 0.1 seconds, how much charge goes through the patient's skin?
The resistance of two conductors of equal cross-sectional area and equal lengths are compared, and are found to be in the ratio 1:2. The resistivities of the materials from which they are constructed must therefore be in what ratio?
A transformer is a device that takes an input voltage and produces an output voltage that can be either larger or smaller than the input voltage, depending on the transformer design. Although the voltage is changed by the transformer, energy is not, so the input power equals the output power. A particular transformer produces an output voltage that is 300 percent of the input voltage. What is the ratio of the output current to the input current?
How many moles of electrons pass through a circuit containing a 100 V battery and a 2 Ω resistor over a period of 10 seconds?
(Note:  )
)
If the area of a capacitor's plates is doubled while the distance between them is halved, how will the final capacitance (Cf) compare to the original capacitance (Ci)?
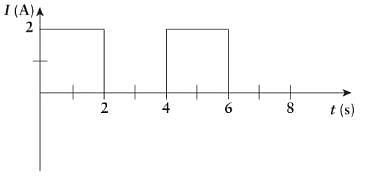
A 10 Ω resistor carries a current that varies as a function of time as shown. How much energy has been dissipated by the resistor after 5 s?
Which of the following will most likely increase the electric field between the plates of a parallel plate capacitor?
Which of the following best characterizes ideal voltmeters and ammeters?
A charge of 2 μC flows from the positive terminal of a 6 V battery, through a 100 Ω resistor, and back through the battery to the positive terminal. What is the total potential difference experienced by the charge?
A voltaic cell provides a current of 0.5 A when in a circuit with a 3 Ω resistor. If the internal resistance of the cell is 0.1 Ω, what is the voltage across the terminals of the battery when there is no current flowing?
|
158 videos|9 docs|21 tests
|