Courses

Test: Cyclic Quadrilaterals


15 Questions MCQ Test Mathematics (Maths) Class 9 | Test: Cyclic Quadrilaterals


Description
This mock test of Test: Cyclic Quadrilaterals for Class 9 helps you for every Class 9 entrance exam. This contains 15 Multiple Choice Questions for Class 9 Test: Cyclic Quadrilaterals (mcq) to study with solutions a complete question bank. The solved questions answers in this Test: Cyclic Quadrilaterals quiz give you a good mix of easy questions and tough questions. Class 9 students definitely take this Test: Cyclic Quadrilaterals exercise for a better result in the exam. You can find other Test: Cyclic Quadrilaterals extra questions, long questions & short questions for Class 9 on EduRev as well by searching above.
QUESTION: 1

In the given figure, ∠M is 75° then ∠O is equal to.

Solution: We know that, sum of all angles of rectangle =360 so, the sum of 2 angles of rectangle = 360\2 = 180  Angle A + Angle B=180  75+B=180 or, B=180-75 or, B=105 degree.
QUESTION: 2

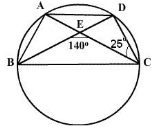
A, B, C and D are four points on a circle. AC and BD intersect at E such that angle BEC =140° and angle ECD = 25°, then angle BAC is

Solution:
QUESTION: 3

ABCD is a cyclic quadrilateral in which AC and BD are its diagonals. If angle DBC = 45° and angle BAC = 30°, the measure of angle BCD is

Solution:
QUESTION: 4

In the figure, triangle ABC is an isosceles triangle with AB = AC and measure of angle ABC = 50°. Then the measure of angle BDC and angle BEC will be
Solution:
QUESTION: 5

In the figure, quadrilateral PQRS is cyclic. If ∠P = 80°, then ∠R =
Solution:
QUESTION: 6

If AB = 12 cm, BC = 16 cm and AB ⊥ BC, then radius of the circle passing through A,B and C is
Solution:

QUESTION: 7

In the figure, ABC is an equilateral triangle. Measure of angle BEC is
Solution:
QUESTION: 8

In the figure, ∠M = 82°, then O = ?
Solution:
QUESTION: 9

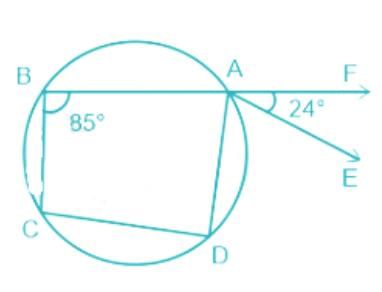
In the figure, ABCD is a cyclic quadrilateral. AF is drawn parallel to CB and DA is produced to point E. If angle ADC = 92°, angle FAE = 20°; then angle BCD will be
Solution:
QUESTION: 10

If ∠C = ∠D = 50° then four points A, B, C, D:
Solution:
QUESTION: 11

In the figure, angle BAD = 75°, angle DCF = x and angle DEF = y.The values of x and y are
Solution:
QUESTION: 12

If the sum of a pair of opposite angles of a quadrilateral is 180o, the quadrilateral is:
Solution:
QUESTION: 13

In the figure, O is the centre of the circle. The measure of angle CBD is
Solution:
QUESTION: 14

ABCD is a cyclic quadrilateral in a circle with centre O. If angle ADC = 130°; then angle BAC is
Solution:
QUESTION: 15

ABC is an isosceles triangle in which AB = AC. If D and E are the mid points of AB and AC respectively, then the points D, B, C and E are
Solution:

Recommended Content

Recommended Tests

Related tests
Follow Us
© EduRev