Test: Data Interpretation - Super TET MCQ
15 Questions MCQ Test - Test: Data Interpretation
Numbers
All numbers used are real numbers.
Figures
A figure accompanying a data sufficiency question will conform to the information given in the question but will not necessarily conform to the additional information given in statements (1) and (2).
Lines shown as straight can be assumed to be straight and lines that appear jagged can also be assumed to be straight.
You may assume that the positions of points, angles, regions, etc. exist in the order shown and that angle measures are greater than zero.
All figures lie in a plane unless otherwise indicated.
Q.
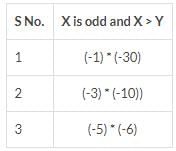
What is the value of X, if X and Y are two distinct integers and their product is 30?
- X is an odd integer
- X > Y
All numbers used are real numbers.
Figures
A figure accompanying a data sufficiency question will conform to the information given in the question but will not necessarily conform to the additional information given in statements (1) and (2).
Lines shown as straight can be assumed to be straight and lines that appear jagged can also be assumed to be straight.
You may assume that the positions of points, angles, regions, etc. exist in the order shown and that angle measures are greater than zero.
All figures lie in a plane unless otherwise indicated.
Q.
Numbers
All numbers used are real numbers.
Figures
A figure accompanying a data sufficiency question will conform to the information given in the question but will not necessarily conform to the additional information given in statements (1) and (2).
Lines shown as straight can be assumed to be straight and lines that appear jagged can also be assumed to be straight.
You may assume that the positions of points, angles, regions, etc. exist in the order shown and that angle measures are greater than zero.
All figures lie in a plane unless otherwise indicated.
Q.
What is the standard deviation (SD) of the four numbers p, q, r, s?
- The sum of p, q, r and s is 24
- The sum of the squares of p, q, r and s is 224
All numbers used are real numbers.
Figures
A figure accompanying a data sufficiency question will conform to the information given in the question but will not necessarily conform to the additional information given in statements (1) and (2).
Lines shown as straight can be assumed to be straight and lines that appear jagged can also be assumed to be straight.
You may assume that the positions of points, angles, regions, etc. exist in the order shown and that angle measures are greater than zero.
All figures lie in a plane unless otherwise indicated.
Q.
Numbers
All numbers used are real numbers.
Figures
A figure accompanying a data sufficiency question will conform to the information given in the question but will not necessarily conform to the additional information given in statements (1) and (2).
Lines shown as straight can be assumed to be straight and lines that appear jagged can also be assumed to be straight.
You may assume that the positions of points, angles, regions, etc. exist in the order shown and that angle measures are greater than zero.
All figures lie in a plane unless otherwise indicated.
Q.
How is Bill related to Betty?
1. Cindy, the wife of Bill's only brother Chris does not have any siblings.
2. Betty is Cindy's brother in law's wife.
All numbers used are real numbers.
Figures
A figure accompanying a data sufficiency question will conform to the information given in the question but will not necessarily conform to the additional information given in statements (1) and (2).
Lines shown as straight can be assumed to be straight and lines that appear jagged can also be assumed to be straight.
You may assume that the positions of points, angles, regions, etc. exist in the order shown and that angle measures are greater than zero.
All figures lie in a plane unless otherwise indicated.
Q.
1. Cindy, the wife of Bill's only brother Chris does not have any siblings.
2. Betty is Cindy's brother in law's wife.
Numbers
All numbers used are real numbers.
Figures
A figure accompanying a data sufficiency question will conform to the information given in the question but will not necessarily conform to the additional information given in statements (1) and (2).
Lines shown as straight can be assumed to be straight and lines that appear jagged can also be assumed to be straight.
You may assume that the positions of points, angles, regions, etc. exist in the order shown and that angle measures are greater than zero.
All figures lie in a plane unless otherwise indicated.
Q.
Is y an integer?
1. y3 is an integer
2. 3y is an integer
Numbers
All numbers used are real numbers.
Figures
A figure accompanying a data sufficiency question will conform to the information given in the question but will not necessarily conform to the additional information given in statements (1) and (2).
Lines shown as straight can be assumed to be straight and lines that appear jagged can also be assumed to be straight.
You may assume that the positions of points, angles, regions, etc. exist in the order shown and that angle measures are greater than zero.
All figures lie in a plane unless otherwise indicated.
Q.
If a salesman received a commission of 3% of the sales that he has booked in a month, what was the sales booked by the salesman in the month of November 2003?
1. The sales booked by the salesman in the month of November 2003 minus salesman's commission was $245,000
2. The selling price of the sales booked by the salesman in the month of November 2003 were 125 percent of the original purchase price of $225,000.
Numbers
All numbers used are real numbers.
Figures
A figure accompanying a data sufficiency question will conform to the information given in the question but will not necessarily conform to the additional information given in statements (1) and (2).
Lines shown as straight can be assumed to be straight and lines that appear jagged can also be assumed to be straight.
You may assume that the positions of points, angles, regions, etc. exist in the order shown and that angle measures are greater than zero.
All figures lie in a plane unless otherwise indicated.
Q.
Is the positive integer m divisible by 6?
1. m is divisible by 3
2. m is divisible by 4
Numbers
All numbers used are real numbers.
Figures
A figure accompanying a data sufficiency question will conform to the information given in the question but will not necessarily conform to the additional information given in statements (1) and (2).
Lines shown as straight can be assumed to be straight and lines that appear jagged can also be assumed to be straight.
You may assume that the positions of points, angles, regions, etc. exist in the order shown and that angle measures are greater than zero.
All figures lie in a plane unless otherwise indicated.
Q.
Is ab positive?
1. (a + b)2 < (a - b)2
2. a = b
Numbers
All numbers used are real numbers.
Figures
A figure accompanying a data sufficiency question will conform to the information given in the question but will not necessarily conform to the additional information given in statements (1) and (2).
Lines shown as straight can be assumed to be straight and lines that appear jagged can also be assumed to be straight.
You may assume that the positions of points, angles, regions, etc. exist in the order shown and that angle measures are greater than zero.
All figures lie in a plane unless otherwise indicated.
Q.
When Y is divided by 2, is the remainder 1?
1. (-1) (Y+2) = -1
2. Y is prime.
Numbers
All numbers used are real numbers.
Figures
A figure accompanying a data sufficiency question will conform to the information given in the question but will not necessarily conform to the additional information given in statements (1) and (2).
Lines shown as straight can be assumed to be straight and lines that appear jagged can also be assumed to be straight.
You may assume that the positions of points, angles, regions, etc. exist in the order shown and that angle measures are greater than zero.
All figures lie in a plane unless otherwise indicated.
Q.
Is the two digit positive integer P a prime number?
1. (P + 2) and (P - 2) are prime.
2. (P - 4) and (P + 4) are prime
Numbers
All numbers used are real numbers.
Figures
A figure accompanying a data sufficiency question will conform to the information given in the question but will not necessarily conform to the additional information given in statements (1) and (2).
Lines shown as straight can be assumed to be straight and lines that appear jagged can also be assumed to be straight.
You may assume that the positions of points, angles, regions, etc. exist in the order shown and that angle measures are greater than zero.
All figures lie in a plane unless otherwise indicated.
Q.
If m, s are the average and standard deviation of integers a, b, c, and d, is s > 0?
1. m > a
2. a + b + c + d = 0
Numbers
All numbers used are real numbers.
Figures
A figure accompanying a data sufficiency question will conform to the information given in the question but will not necessarily conform to the additional information given in statements (1) and (2).
Lines shown as straight can be assumed to be straight and lines that appear jagged can also be assumed to be straight.
You may assume that the positions of points, angles, regions, etc. exist in the order shown and that angle measures are greater than zero.
All figures lie in a plane unless otherwise indicated.
Q.
Is x3 > x2 ?
1. x > 0
2. x < 1
Numbers
All numbers used are real numbers.
Figures
A figure accompanying a data sufficiency question will conform to the information given in the question but will not necessarily conform to the additional information given in statements (1) and (2).
Lines shown as straight can be assumed to be straight and lines that appear jagged can also be assumed to be straight.
You may assume that the positions of points, angles, regions, etc. exist in the order shown and that angle measures are greater than zero.
All figures lie in a plane unless otherwise indicated.
Q.
Is y = 3?
1. (y - 3)(x - 4) = 0
2. (x - 4) = 0
Numbers
All numbers used are real numbers.
Figures
A figure accompanying a data sufficiency question will conform to the information given in the question but will not necessarily conform to the additional information given in statements (1) and (2).
Lines shown as straight can be assumed to be straight and lines that appear jagged can also be assumed to be straight.
You may assume that the positions of points, angles, regions, etc. exist in the order shown and that angle measures are greater than zero.
All figures lie in a plane unless otherwise indicated.
Q.
Is x/y a terminating decimal?
1. x is a multiple of 2
2. y is a multiple of 3
Numbers
All numbers used are real numbers.
Figures
A figure accompanying a data sufficiency question will conform to the information given in the question but will not necessarily conform to the additional information given in statements (1) and (2).
Lines shown as straight can be assumed to be straight and lines that appear jagged can also be assumed to be straight.
You may assume that the positions of points, angles, regions, etc. exist in the order shown and that angle measures are greater than zero.
All figures lie in a plane unless otherwise indicated.
Q.
Is the positive integer X divisible by 21?
1. When X is divided by 14, the remainder is 4
2. When X is divided by 15, the remainder is 5
Numbers
All numbers used are real numbers.
Figures
A figure accompanying a data sufficiency question will conform to the information given in the question but will not necessarily conform to the additional information given in statements (1) and (2).
Lines shown as straight can be assumed to be straight and lines that appear jagged can also be assumed to be straight.
You may assume that the positions of points, angles, regions, etc. exist in the order shown and that angle measures are greater than zero.
All figures lie in a plane unless otherwise indicated.
Question: What is the value of b?
1) a = 3
2) (a-3)(b+2)=0