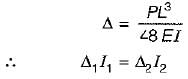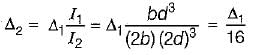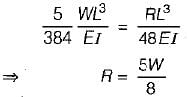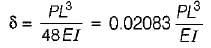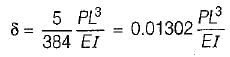Test: Deflection & Theories of Failure - 1 - Mechanical Engineering MCQ
10 Questions MCQ Test - Test: Deflection & Theories of Failure - 1
A simply supported beam of span L carries a point load Pat the mid span. The downward deflection under the load will be
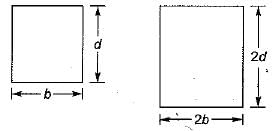
A simply supported beam carries a concentrated load P at the mid span and experiences a maximum deflection Av Subsequently, the breadth and depth of beam is doubled. The corresponding deflection under the load will become
A simply supported beam carries a total load W which is uniformly distributed on the entire span. The center of beam is propped so that it is brought to the level of end supports. The prop reaction would be
A point load placed at the mid span of a simply supported beam has been replaced by a uniformly distributed load of same total value. The central deflection in the later case will be
A cantilevel beam of length L is subjected to a concentrated load Pat a distance of L/3 from the free end. What is the deflection at free end of the beam?
Which amongst the following methods is/are most commonly used to determine beam deflection?
1. Double-integration method
2. Method of singularity functions
3. Elastic energy methods
4. Moment-area methods
The differential equation of the bent beam is given by
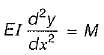
The significance of this equation is, except
A support is said to be non-yielding if
A simply supported beam has been subjected to unsymmetrical loading. The deflection would be maximum at a section where
Which of the following statements pertaining to slope of loaded beam is WRONG? The maximum slope