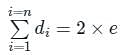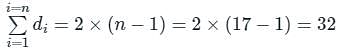Test: Degree of Vertex - Civil Engineering (CE) MCQ
10 Questions MCQ Test Engineering Mathematics - Test: Degree of Vertex
In an undirected graph, if we add the degrees of all vertices, it is:
What is the sum of the degree of each vertex for an undirected graph with m vertices and n edges ?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The maximum degree of any vertex in a simple graph with n vertices is
The degree sequence of a simple graph is the sequence of the degree of the nodes in the graph in decreasing order. Which of the following sequence can be the degree sequence of any graph?
I. 4 7 1 6 3 4 6 2
II. 3 3 3 3 3 3
III. 5 4 6 7 6 3 6 5
An undirected graph G with only one simple path between each pair of vertices has two vertices of degree 4, one vertex of degree 3 and two vertices of degree 2.
Number of vertices of degree 1 are ______________
Consider n-dimensional cube and its complement graph represented by ‘G’ and ‘H’ respectively. y × 210 edges are present in graph ‘H’ if ‘n’ is equal to 11. Find the value of y?
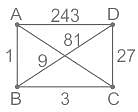
Consider a 4-ary tree T consisting of 17 vertices. What is the sum of the degree of T?
Which of the following can be degree sequence of simple graph?
I. 2, 3, 3, 3, 3, 3, 4, 5
II. 1, 3, 3, 4, 5, 6, 6
III. 1, 1, 3, 3, 5, 6, 7
IV. 1, 2, 3, 3, 4, 5, 6
If for some positive integer k, degree of vertex d(v)=k for every vertex v of the graph G, then G is called ______.
|
65 videos|120 docs|94 tests
|
|
65 videos|120 docs|94 tests
|