Test: Digital Filters Design Consideration - Electronics and Communication Engineering (ECE) MCQ
10 Questions MCQ Test Digital Signal Processing - Test: Digital Filters Design Consideration
The ideal low pass filter cannot be realized in practice.
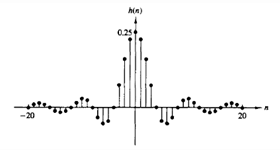
The following diagram represents the unit sample response of which of the following filters?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If h(n) has finite energy and h(n)=0 for n<0, then which of the following are true?
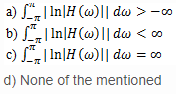
If |H(ω)| is square integrable and if the integralis finite, then the filter with the frequency response
The magnitude function |H(ω)| can be zero at some frequencies, but it cannot be zero over any finite band of frequencies.
If h(n) is causal and h(n)=he(n)+ho(n),then what is the expression for h(n) in terms of only he(n)?
If h(n) is causal and h(n)=he(n)+ho(n),then what is the expression for h(n) in terms of only ho(n)?
If h(n) is absolutely summable, i.e., BIBO stable, then the equation for the frequency response H(ω) is given as?
HR(ω) and HI(ω) are interdependent and cannot be specified independently when the system is causal.
|
3 videos|50 docs|54 tests
|
|
3 videos|50 docs|54 tests
|

















