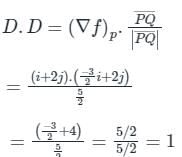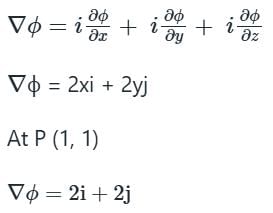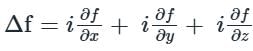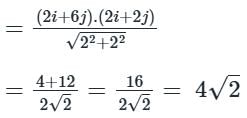Test: Directional Derivatives - Engineering Mathematics MCQ
15 Questions MCQ Test - Test: Directional Derivatives
The directional derivative of ϕ = xy + yz + zx along the tangent to the curve at x = t, y = t2, z = t3 at P(1,1,1) is A/√14, then the value of A is:
The directional derivative of f(x, y, z) = x(x2 - y2) - z at A(1, -1, 0) in the direction of p̅ = (2î - 3ĵ + 6k̂) is:
The directional derivative of r7 in the direction of 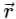 at (1, -1, 1) will be ________
at (1, -1, 1) will be ________
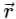 at (1, -1, 1) will be ________
at (1, -1, 1) will be ________The directional derivative of f(x, y, z) = xyz at point (-1, 1, 3) in the direction of vector î - 2ĵ + 2k̂ is
The maximum value of the directional derivative of the function ϕ = 2x2 + 3y2 + 5z2 at point (1, 1, -1) is
The value of the directional derivative of the function θ (x, y, z) = xy2 + yz2 + zx2 at the point (2, -1, 1) in the direction of the vector p = i + 2j + 2k is
The directional derivative of the function f(x, y) = x2 + y2 along a line directed from (0,0) to (1,1), evaluated at the point x = 1, y = 1 is
The smaller angle (in degrees) between the planes x + y + z = 1 and 2x - y + 2z = 0 is __________.
If |p̅ (s)| is a non-zero constant, then direction of 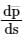
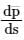 is:
is:
Find the greatest value of the directional derivatives of the function f = x2yz3 at (2, 1, -1) is
The directional derivative of 1/r in the direction of 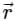 is
is
At point (1, 0, 3) on the surface 2x2 + 3y2 + z2 – 11 = 0, the directional derivative in the direction
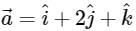 is
is
The magnitude of the directional derivative of the function f(x, y) = x2 + 3y2 in a direction normal to the circle x2 + y2 = 2, at the point (1, 1), is
A function is defined in Cartesian coordinate system as f(x, y) = xey. The value of the directional derivative of the function (in integer) at the point (2, 0) along the direction of the straight line segment from point (2, 0) to point (1/2, 2) is ______
The magnitude of the directional derivative of the function f(x, y) = x2 + 3y2 in a direction normal to the circle x2 + y2 = 2, at the point (1, 1), is


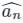
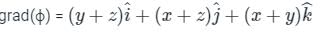
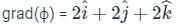
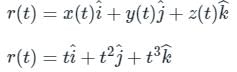
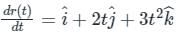
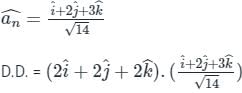
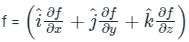
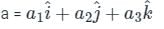
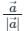
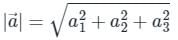
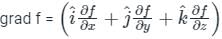
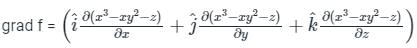
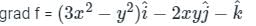
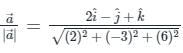
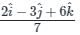
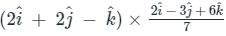
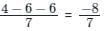

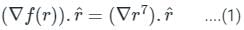
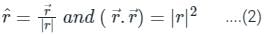
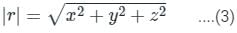
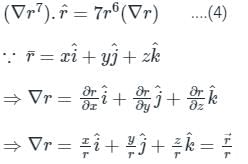
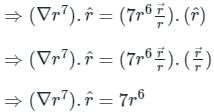
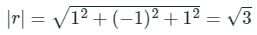
 at (1, -1, 1),
at (1, -1, 1), 
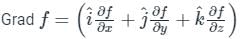
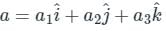

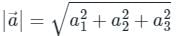
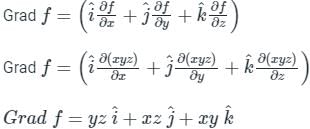
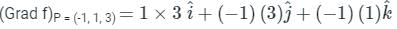
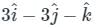
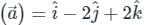
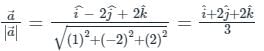
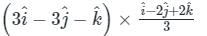
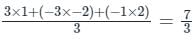
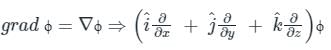
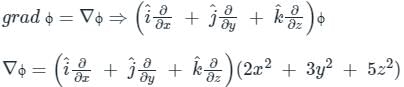
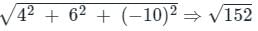
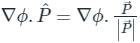
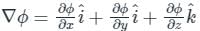
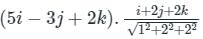
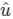 is given by
is given by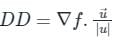
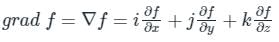
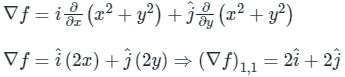
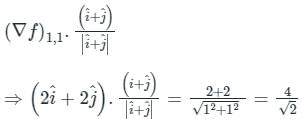
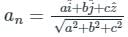
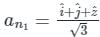 and
and 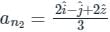 respectively.
respectively.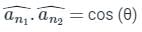
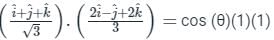
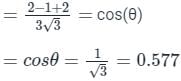
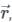 , there are two parts one is the direction and the other is magnitude.
, there are two parts one is the direction and the other is magnitude.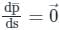 , i.e., zero vector.
, i.e., zero vector.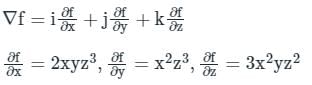

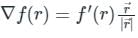
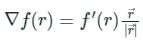
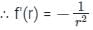
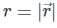
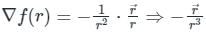
 . It will be given by:
. It will be given by: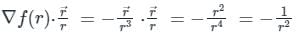
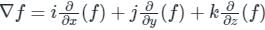
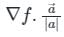
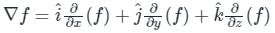
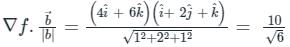

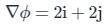
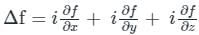
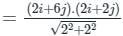
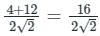
 ) Converts vector function to scalar (Dot product)
) Converts vector function to scalar (Dot product) ) converts vector function to vector function (Cross product)
) converts vector function to vector function (Cross product)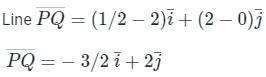
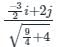
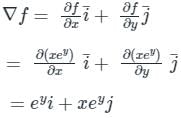
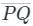 is
is