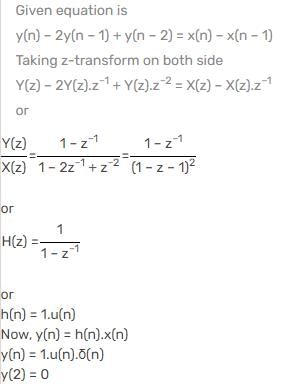Test: Discrete-Time Fourier Transform
10 Questions MCQ Test Signals and Systems | Test: Discrete-Time Fourier Transform
| 1 Crore+ students have signed up on EduRev. Have you? |
Given a discrete time signal x[k] defined by x[k] = 1, for -2 ≤ k ≤ 2 and 0, for |k| > 2. Then, y[k] = x[3k - 2] is ______________
y[k] = x [3k-2]
Now, y [0] = x [-2] = 1
Or, y [1] = x [1] = 1
Or, y [2] = x [4] = 0
∴ y[k] = 1, for k = 0, 1 and 0 otherwise.
A discrete time signal is given as X [n]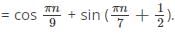 
The period of the signal X [n] is ______________
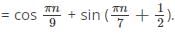The period of the signal X [n] is ______________Given that, N1 = 18, N2 = 14
We know that period of X [n] (say N) = LCM (N1, N2)
∴ Period of X [n] = LCM (18, 14) = 126.
F(t) and G(t) are the one-sided z-transforms of discrete time functions f(nt) and g(nt), the z-transform of ∑f(kt)g(nt-kt) is given by _____________
Given that F (t) and G (t) are the one-sided z-transforms.
Also, f (nt) and g (nt) are discrete time functions, which means that property of Linearity, time shifting and time scaling will be similar to that of continuous Fourier transform. Since, for a continuous Fourier transform, the value of ∑f(kt)g(nt-kt) is given by∑f(nt)g(nt)z-n.
∴ z-transform of ∑f(kt)g(nt-kt) is given by∑f(nt)g(nt)z-n.
A Discrete signal is said to be even or symmetric if X(-n) is equal to __________
We know that any signal be it discrete or continuous is said to be even or symmetric when that signal f(x) = f (-x). Here given signal is X (n). It is a discrete time signal. So, the signal will be even symmetric if X (n) = X (-n).
A discrete time signal is as given below
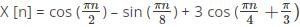
The period of the signal X [n] is _____________
Given that, N1 = 4, N2 = 16, N3 = 8
We know that period of X [n] (say N) = LCM (N1, N2, N3)
∴ Period of X [n] = LCM (4, 16, 8) = 16.
The time system which operates with a continuous time signal and produces a continuous time output signal is _________
DTF System operates with a discrete signal, on the other hand time invariant system is a system whose output does not depend explicitly on time. For continuous time system, the inputs as well as output both are CT signals.
What is the steady state value of The DT signal F (t), if it is known that F(s)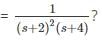 
The steady state value of the DT signal F(s) exists since all poles of the given Laplace transform have negative real part.
∴F (∞) = lims→0 s F(s)
= 0.
A discrete time signal is as given below X [n] = cos (n/8) cos (πn/8)
The period of the signal X [n] is _____________
We know that for X [n] = X1 [n] × X2 [n] to be periodic, both X1 [n] and X2 [n] should be periodic with finite periods.
Here X2 [n] = cos (πn/8), is periodic with fundamental period as 8/n
But X1 [n] = cos (n/8) is non periodic.
∴ X [n] is a non-periodic signal.
The system described by the difference equation y(n) – 2y(n-1) + y(n-2) = X(n) – X(n-1) has y(n) = 0 and n<0. If x (n) = δ(n), then y (z) will be?
Given equation = y (n) – 2y (n-1) + y (n-2) = X (n) – X (n-1) has y (n) = 0
For n = 0, y (0)2y (-1) + y (-2) = x (0) – x (-1)
∴ y(0) = x(0) – x(-1)
Or, y (n) = 0 for n<0
For n=1, y (1) = -2y (0) + y (-1) = x (1) – x (0)
Or, y (1) = x (1) – x (0) + 2x (0) – 2x (-1)
Or, y (1) = x (1) +x (0) – 2x (-1)
For n=2, y (2) = x (2) – x (1) + 2y (1) – y (0)
Or, y(2) = x(2) – x(1) + 2x(1) + 2x(0) – 4x(-1) – x(0) + x(-1)
∴y (2) = d (2) + d (1) + d (0) – 3d (-1).
The Nyquist frequency for the signal x (t) = 3 cos 50πt + 10 sin 300πt – cos 100t is ___________
We know that Nyquist frequency is twice the maximum frequency, i.e. fs = 2 fm.
The maximum frequency present in the signal is ωm = 300 π or fm = 150 Hz. Therefore the Nyquist frequency fs = 2 fm = 300 Hz.
|
40 videos|44 docs|33 tests
|
|
Use Code STAYHOME200 and get INR 200 additional OFF
|
Use Coupon Code |
|
40 videos|44 docs|33 tests
|
Download free EduRev App
Related content with Test: Discrete-Time Fourier Transform
|
|
|
|
Related tests with Test: Discrete-Time Fourier Transform
|
|
|
|
|
|
© EduRev
|
Education Revolution
|
Follow Us
|
