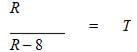Test: Distance And Speed- 3 - GMAT MCQ
10 Questions MCQ Test - Test: Distance And Speed- 3
Bob bikes to school every day at a steady rate of x miles per hour. On a particular day, Bob had a flat tire exactly halfway to school. He immediately started walking to school at a steady pace of y miles per hour. He arrived at school exactly t hours after leaving his home. How many miles is it from the school to Bob's home?
Lexy walks 5 miles from point A to point B in one hour, then bicycles back to point A along the same route at 15 miles per hour. Ben makes the same round trip, but does so at half of Lexy’s average speed. How many minutes does Ben spend on his round trip?
Triathlete Dan runs along a 2-mile stretch of river and then swims back along the same route. If Dan runs at a rate of 10 miles per hour and swims at a rate of 6 miles per hour, what is his average rate for the entire trip in miles per minute?
Tom and Linda stand at point A. Linda begins to walk in a straight line away from Tom at a constant rate of 2 miles per hour. One hour later, Tom begins to jog in a straight line in the exact opposite direction at a constant rate of 6 miles per hour. If both Tom and Linda travel indefinitely, what is the positive difference, in minutes, between the amount of time it takes Tom to cover half of the distance that Linda has covered and the amount of time it takes Tom to cover twice the distance that Linda has covered?
It takes the high-speed train x hours to travel the z miles from Town A to Town B at a constant rate, while it takes the regular train y hours to travel the same distance at a constant rate. If the high-speed train leaves Town A for Town B at the same time that the regular train leaves Town B for Town A, how many more miles will the high-speed train have traveled than the regular train when the two trains pass each other?
The ‘moving walkway’ is a 300-foot long conveyor belt that moves continuously at 3 feet per second. When Bill steps on the walkway, a group of people that are also on the walkway stands 120 feet in front of him. He walks toward the group at a combined rate (including both walkway and foot speed) of 6 feet per second, reaches the group of people, and then remains stationary until the walkway ends. What is Bill’s average rate of movement for his trip along the moving walkway?
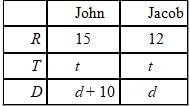
John and Jacob set out together on bicycle traveling at 15 and 12 miles per hour, respectively. After 40
minutes, John stops to fix a flat tire. If it takes John one hour to fix the flat tire and Jacob continues to ride during this time, how many hours will it take John to catch up to Jacob assuming he resumes his ride at 15 miles per hour? (consider John's deceleration/acceleration before/after the flat to be negligible)
Deb normally drives to work in 45 minutes at an average speed of 40 miles per hour. This week, however, she plans to bike to work along a route that decreases the total distance she usually travels when driving by 20% . If Deb averages between 12 and 16 miles per hour when biking, how many minutes earlier will she need to leave in the morning in order to ensure she arrives at work at the same time as when she drives?
Alex and Brenda both stand at point X. Alex begins to walk away from Brenda in a straight line at a rate of 4 miles per hour. One hour later, Brenda begins to ride a bicycle in a straight line in the opposite direction at a rate of R miles per hour. If R > 8, which of the following represents the amount of time, in terms of R, that Alex will have been walking when Brenda has covered twice as much distance as Alex?
On Monday, Lou drives his ford escort with 28-inch tires, averaging x miles per hour. On Tuesday, Lou
switches the tires on his car to 32-inch tires yet drives to work at the same average speed as on Monday. What is the percent change from Monday to Tuesday in the average number of revolutions that Lou’s tires make per second?



 and as high speed train takes x hours which will definitely be lesser than the time taken by a normal train which is y hours, So y>x
and as high speed train takes x hours which will definitely be lesser than the time taken by a normal train which is y hours, So y>x