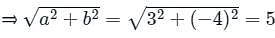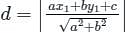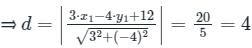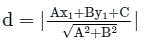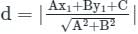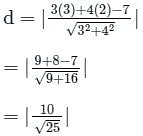Test: Distance of a Point from a Line (7 July) - JEE MCQ
10 Questions MCQ Test Daily Test for JEE Preparation - Test: Distance of a Point from a Line (7 July)
The product of the perpendiculars from the two points (±4, 0) to the line 3x cos ϕ + 5y sin ϕ = 15 is
The distance of the point of intersection of the lines 2x - 3y + 5 = 0 and 3x + 4y = 0 from the line 5x - 2y = 0 is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Find the values of k for which the length of the perpendicular from the point (4, 1) on the line 3x - 4y + k = 0 is 2 units ?
The point on y-axis equidistant from the points (3,2) and (-1,3) is
The pair of lines 3x + 2y = 5, 2x - 3y = 7 are
Find the perpendicular distance of the line 3y = 4x + 5 from (2, 1)
What is the perpendicular distance from the point (2, 3, 4) to the line 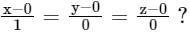
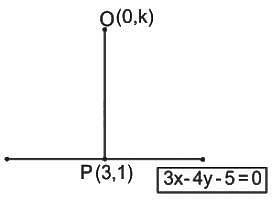
If the foot of the perpendicular drawn from the point (0, k) to the line 3x - 4y - 5 = 0 is (3, 1), then what is the value of k?
Find the distance of the point (4, 1) from the line 3x - 4y + 12 = 0 ?
The distance of a point (3, 2) from a line 3x + 4y = 7 is
|
360 tests
|


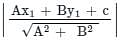
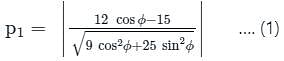
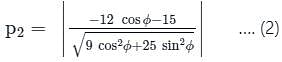
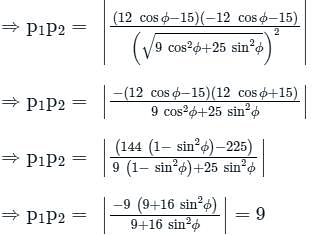
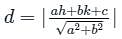

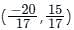
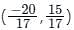 from the line 5x - 2y = 0 is
from the line 5x - 2y = 0 is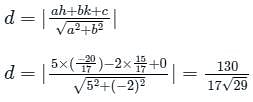
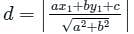
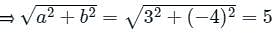
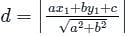

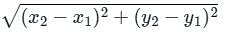
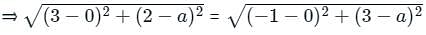
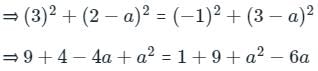
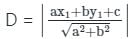
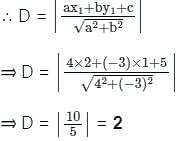
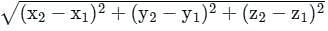
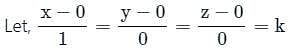
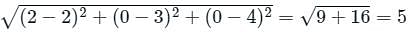


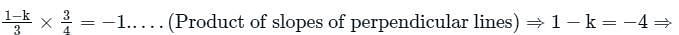 K = 5
K = 5