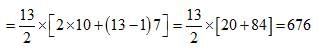Test: Divisibility And Remainders- 3 - GRE MCQ
10 Questions MCQ Test Quantitative Reasoning for GRE - Test: Divisibility And Remainders- 3
What is the smallest integer that is multiple of 5, 7, and 20?
Which of these numbers is not divisible by 3?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
What is the smallest positive 2-digit whole number divisible by 3 and such that the sum of its digits is 9?
Let n! = 1 x 2 x 3 x……….x n for integer n> 1. If p = 1! + (2 x 2!) + (3 x 3!) + ……(10 x 10!),then p+2 when divided by 11! Leaves remainder of
The remainder, when (1523 + 2323) is divided by 19, is :
What is the sum of all two-digit numbers that give a remainder of 3 when they are divided by 7?
What is the remainder when 1044 × 1047 × 1050 × 1053 is divided by 33?
If a positive integer n is divided by 5, the remainder is 3. Which of the numbers below yields a remainder of 0 when it is divided by 5?
If an integer n is divisible by 3, 5, and 12, what is the next larger integer divisible by all these numbers?
If n is an integer, when (2n + 2)2 is divided by 4 the remainder is
|
93 videos|77 docs|104 tests
|
|
93 videos|77 docs|104 tests
|