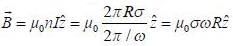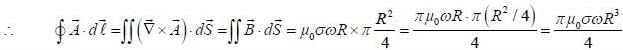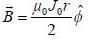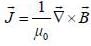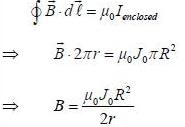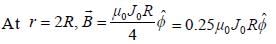Test: EMT - Magnetostatics - Physics MCQ
20 Questions MCQ Test GATE Physics Mock Test Series 2025 - Test: EMT - Magnetostatics
Which one of the following can represent the magnetic field outside the wire of radius a earning an arbitrary current distribution in its volume:
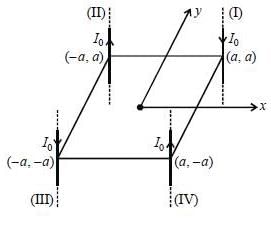
Suppose four infinitely long wires passing through the corners of a square of side 2a centre at origin in x-y plane as shown in figure. The magnetic tield at origin is

| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A long wire of radius R carries a current I with a volume current density 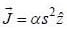 (where α is a constant and s is the perpendicular distance from the axis). The value of α is
(where α is a constant and s is the perpendicular distance from the axis). The value of α is
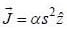 (where α is a constant and s is the perpendicular distance from the axis). The value of α is
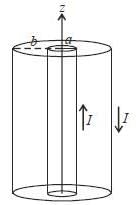
(where α is a constant and s is the perpendicular distance from the axis). The value of α isA long hollow coaxial wire lias inner radius a and outer radius b. Uniform current I flows along its inner surface and return through the outer surface as shown in figure. The magnitude vector potential in different regions are
A conducting wire carrying current I0 is bent in the shape of a loop, as shown in figure. The magnetic field at Unseen point O is given by

A vector potntial at a point is given by 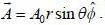 The current density corresponding to the vector potential is
The current density corresponding to the vector potential is
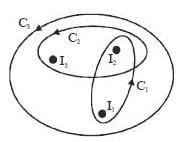
Three infinitely-long conductors carrying currents I1, I2, and I3 lie perpendicular to the plane of the paper as shown below. If the value of integral  for the loops C1, C2, and C3 are 2μ0, 4μ0 and μ0 in the units of N/A, respectively, then
for the loops C1, C2, and C3 are 2μ0, 4μ0 and μ0 in the units of N/A, respectively, then
If a point dipole of the dipole moment 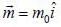 is kept in external magnetic field
is kept in external magnetic field 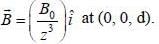 The force acting on the dipole is given by
The force acting on the dipole is given by
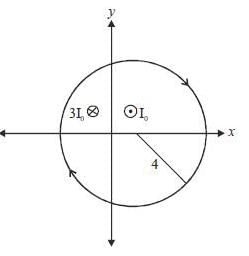
Consider two infinitely Ions wires parallel to the z-axis passing through the point 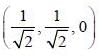 and
and 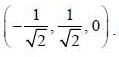 One is carrying current I0 along positive z-direction of other one is carrying current 3I0, along negative z-direetion. The value of
One is carrying current I0 along positive z-direction of other one is carrying current 3I0, along negative z-direetion. The value of 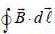 on closed curve (x - 1)2 + y2 = 16 along clockwise direction is _____ μ0I0.
on closed curve (x - 1)2 + y2 = 16 along clockwise direction is _____ μ0I0.
(Answer should be integer).
An election is revolving around the nucleus in circular orbit of radius a0 in a hydrogen atom. If electron is revolving with speed v0 , the magnetic field at nucleus due to orbital motion of electron is 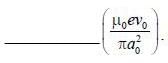 . (Round off to two decimal places)
. (Round off to two decimal places)
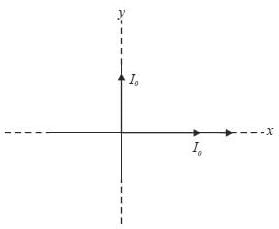
Two infintely long current carrying wire are placed along x and y axis and crossing through the origin as shown in figure. The magnetic field at (2, 3,4) will be
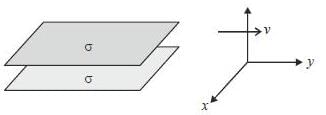
Two large parallel plates move with a constant speed v in the positive y direction as shown in figure. If both the plates have surface charge density σ, the magnetic force per unit area on the lower plate is
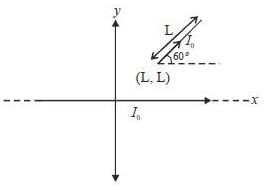
All infinitely long wire carrying current I0 is placed (crossing through the origin) along x-axis and another wire of length L carrying current I0 is placed mx-y plane, as shown in figure below. Thex-component of magnetic force acting on the wire is given by
The regions of space z < 0 and z > 0 are filled with free space and material having permeability 2μ0 respectively. The magnetic field m the region 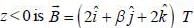 and the magnitude of magnetic field in region z > 0 is 6T. The angle between magnetic field and normal to the mterface in region z < 0 is given by
and the magnitude of magnetic field in region z > 0 is 6T. The angle between magnetic field and normal to the mterface in region z < 0 is given by
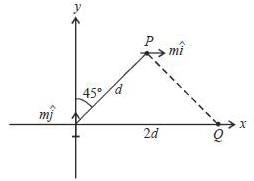
Two magnetic dipoles of magnitude m, one is placed at origin and the otherone is displaced from P to Q keeping the direction fixed (Assume that P and Q both are in x-y plane). The required work done to displaced the magnetic dipole from P to Q is
A ring of radius R carries a linear charge density λ. It is rotating about an axis crossing through its centre and perpendicular to its plane with an angular speed ω. The magnetic field on its axis at a distance 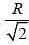 from the centre is ________ μ0λω. (Round off to two decimal places)
from the centre is ________ μ0λω. (Round off to two decimal places)
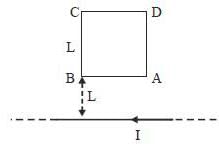
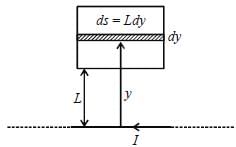
A rigid square loop ABCD of side L is situated at a distance L from an infinite straight wire, with the side AB parallel to the infinite wire, as shown in the figure below. The infinite wire, which is in the plane of the loop, carries a current I from right to left. The value of 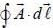 through the square loop is _____________
through the square loop is _____________ 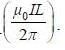 (Round off to two decimal places)
(Round off to two decimal places)
The volume current density through a long cylindrical conductor is given to be 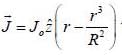 where, R is radius of cylinder and r is tlie distance of some point from tlie axis of cylinder and J0 is a constant. The value of r at which magnetic field maximum is ___________________ R. (Round off to two decimal places)
where, R is radius of cylinder and r is tlie distance of some point from tlie axis of cylinder and J0 is a constant. The value of r at which magnetic field maximum is ___________________ R. (Round off to two decimal places)
A long hollow cylinder of radius R carrying uniform surface charge density σ. It is rotating about its axis with angular speed ω. A ring of radius (r = R/2) is placed eo-axially with cylinder. The value of 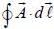 ton the ring is ______ πμ0ωσR3 (Round off to two decimal places)
ton the ring is ______ πμ0ωσR3 (Round off to two decimal places)
A long solid conducting cylinder of radius R carrying volume current along its axis. The magnetic field inside the cylinder is given by 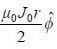 (where J0 is a constant and r is the distance from the it axis). The magnetic field at a distance r = 2R from it axis is______
(where J0 is a constant and r is the distance from the it axis). The magnetic field at a distance r = 2R from it axis is______ 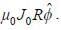
(Upto two decimal places)
|
1 docs|34 tests
|


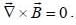
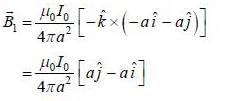
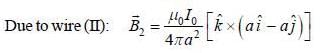
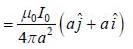
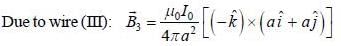
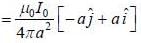
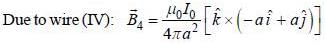
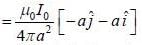
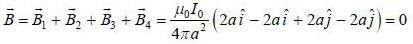
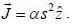

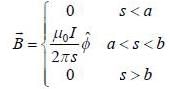
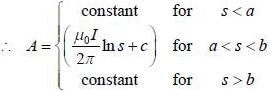
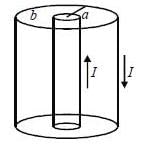
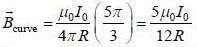
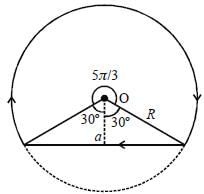
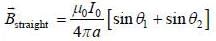
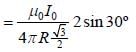

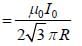
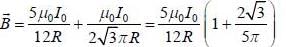
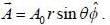
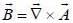
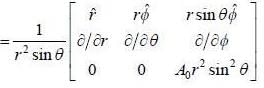
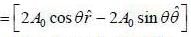
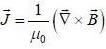
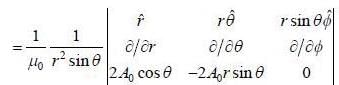
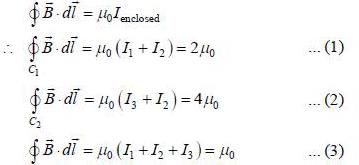
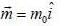
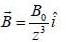
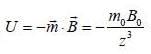

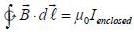



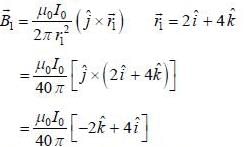
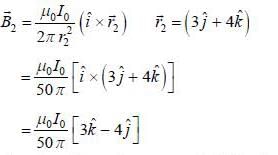
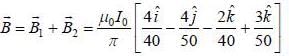
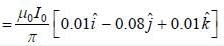
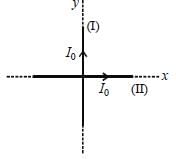
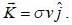
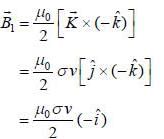
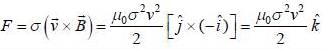
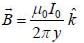
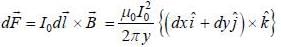
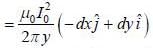

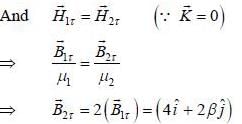
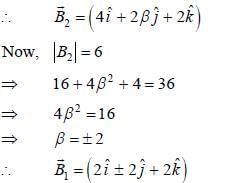
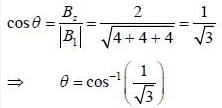
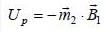
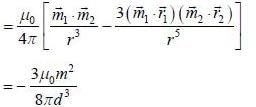

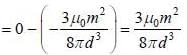
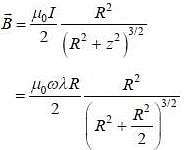
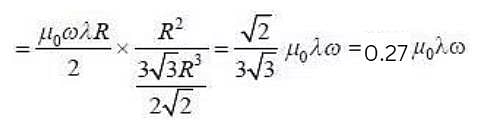
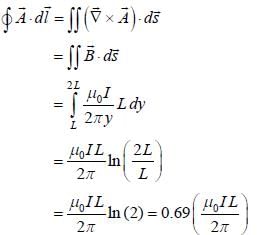


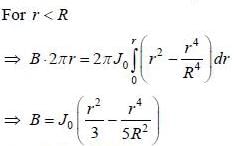
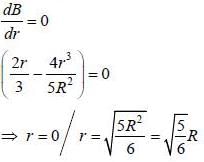
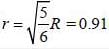
 and we can treat it as solenoid.
and we can treat it as solenoid.