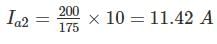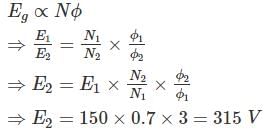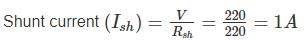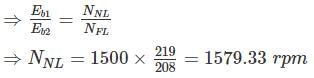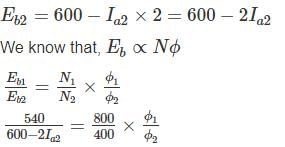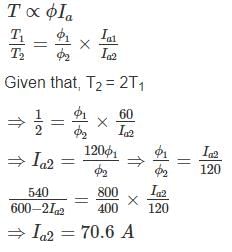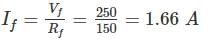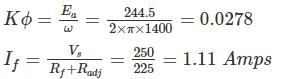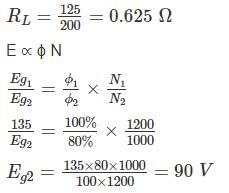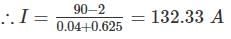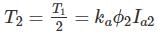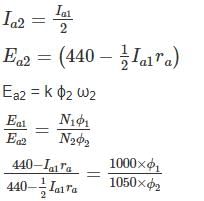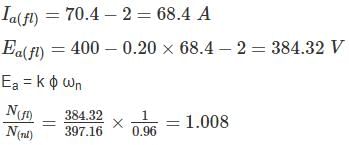Test: Electrical Machines- 4 - Electrical Engineering (EE) MCQ
10 Questions MCQ Test - Test: Electrical Machines- 4
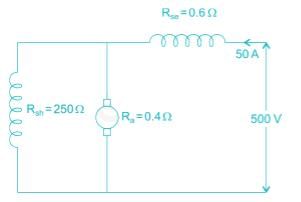
A short shunt compound wound motor is having series field resistance, armature resistance and shunt field resistance of 0.6 Ω, 0.4 Ω and 250 Ω respectively. If the motor is drawing 50 A at 500 V, what the voltage drop across series field resistance?
A DC shunt motor of 200 V, 10.5 A, 2000 rpm has an armature resistance of 0.5 Ω and field resistance of 400 Ω. It drives a load whose torque is constant at rated motor torque. What is the value of armature current if the source voltage drops to 175 V?
A six pole, 60 kW DC machine operating at 1200 rpm has a generated emf of 150 V. If the speed is reduced to 70% of its original value and the pole flux is tripled, then induced emf would be___ (in V)
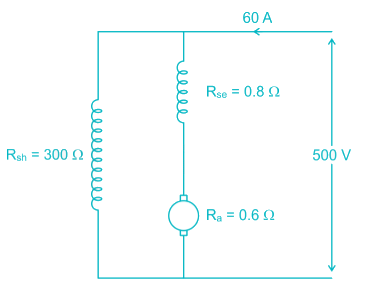
A long shunt compound wound motor is having shunt field resistance, series field resistance and armature resistance of 300 Ω, 0.8 Ω and 0.6 Ω respectively. If the motor is drawings 60 A at 500 V, what is the voltage drop across series field resistance?
A 220 V DC shunt motor takes 3 A at no-load. It draws 25 A when running at full-load at 1500 rpm. The armature and shunt resistances are 0.5 Ω and 220 Ω, respectively. The no- load speed in rpm (round off to two decimal places) is ________.
A 600 V series motor of resistance 1 Ω runs at 800 rpm when the current is 60 A. If an identical motor is mechanically coupled and joined in series, what will be the current (in A) when the set runs at 400 rpm and exerts twice the original gross torque?
A 250-V DC shunt motor has a shunt field resistance of 150 Ω and an armature resistance of 0.3 Ω. For a given load. The motor runs at 1400 rpm, and drawing 20 A current. If a resistance of 75 Ω is added in series with the field, find the new armature current (in A). Assume load torque and flux and constant.
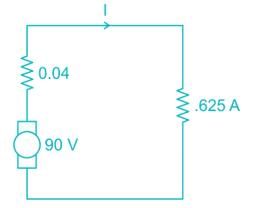
A separately excited DC generator, when running at 1200 rpm supplies 200 A at 125 V to a circuit of constant resistant what will be the current (in amp) when the speed is dropped to 1000 rpm and the field is reduced to 80%. Armature resistance is 0.04 Ω and total drop at brushes is 2V.
A 440 V DC shunt motor is running at 1000 RPM at full load torque, reduced armature voltage and full field. If load torque is reduced to 50% of rated value with armature voltage and field voltage held constant at previous value, the speed increase 1050 rpm. Find armature voltage drop (in V) at full load. Neglect effect of armature reaction. [Take no load speed 1000 rpm]
A 400 V dc shunt motor takes a current of 6.2 A on no load and 70.4 A on full - load. Armature reaction weakens the field by 4%. Calculate the ratio of full-load speed to no-load speed. Given Ra = 0.20 Ω, Brush voltage drop = 2 V, Rf = 200 Ω.