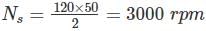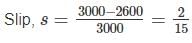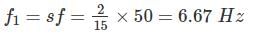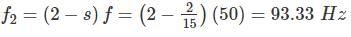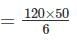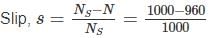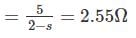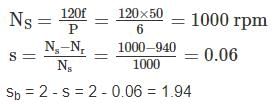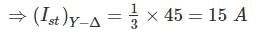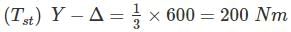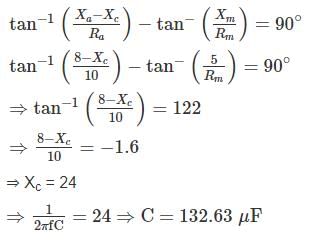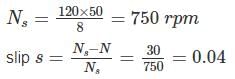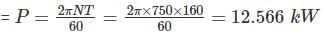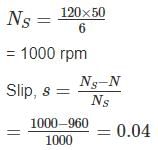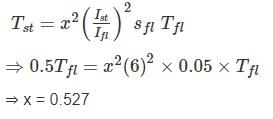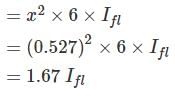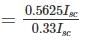Test: Electrical Machines- 6 - Electrical Engineering (EE) MCQ

A 50 Hz, 6 pole, single phase induction motor is rotating in the clockwise direction at a speed of 940 rpm. The slip of motor in the direction of rotation and opposite direction of motor will be respectively.

The starting current and torque of a three phase induction motor on direct line starting is 45 A and 600 Nm respectively. What are the corresponding values with star delta starter.

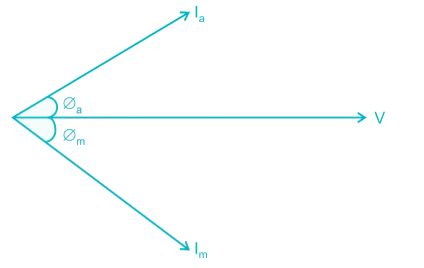
The value of the starting capacitor required to produce 90° phase difference between the currents in the main and auxiliary windings will be – (in μF)

An 8 pole 40 kW, 125 V, 50 Hz single phase motor is running at speed at 720 rpm with forward field torque of 200 N-m end backward field torque of 40 N-m. If friction and winding losses are 20 w, what is the mechanical power output in watts?

A 6 pole, 350 W, 110 V, 50 Hz single phase motor is running at 960 rpm with forward field torque of 220 N-m and backward field torque of 30 N-m. If friction and winding losses are 10 W, What is the mechanical power output?

Determine the current drawn from the main as a fraction of full load current of an auto transformer starter for an induction motor required to start the motor with 50 percent of full-load torque. The short circuit current of the motor is 6 times the full load current and full load slip is 0.05.

A induction motor is started in first case by autotransformer with 3/4^th tapping and is second case by a star delta starter. What is the ratio of supply current at starting of first case to second one upto two decimal places