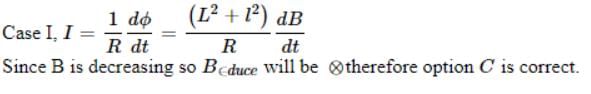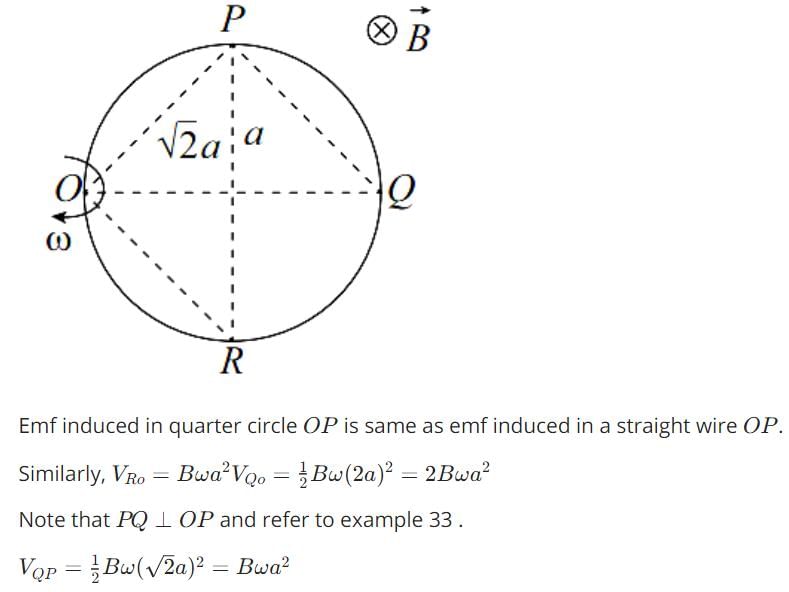Test: Electromagnetic Induction - 2
25 Questions MCQ Test Physics Class 12 | Test: Electromagnetic Induction - 2
| 1 Crore+ students have signed up on EduRev. Have you? |
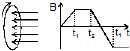
A wire loop is placed in a region of time varying magnetic field which is oriented orthogonally to the plane of the loop as shown in the figure. The graph shows the magnetic field variation as the function of time. Assume the positive emf is the one which drives a current in the clockwise direction and seen by the observer in the direction of B. Which of the following graphs best represents the induced emf as a function of time.
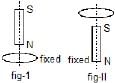
A vertical bar magnet is dropped from position on the axis of a fixed metallic coil as shown in fig-I. In fig-II the magnet is fixed and horizontal coil is dropped. The acceleration of the magnet and coil are a1 and a2 respectively then
An electric current i1 can flow either direction through loop (1) and induced current i2 in loop (2). Positive i1 is when current is from `a' to `b' in loop (1) and positive i2 is when the current is from `c' to `d' in loop (2)
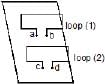
In an experiment, the graph of i2 against time `t' is as shown below
Which one(s) of the following graphs could have caused i2 to behave as give above.
ϕ2=Mi1⇒i2=(1/R)(−dϕ2/dt)
i2=−MdI1/Rdt
Figure shows a bar magnet and a long straight wire W, carrying current into the plane of paper. Point P is the point of intersection of axis of magnet and the line of shortest distance between magnet and the wire. If p is the midpoint of the magnet, then which of the following statements is correct ?
There is a long straight wire W, the current flowing direction in the wire is into the plane of paper and the point of intersection on the axis of magnet is P.
If the midpoint of the bar magnet is P then the distance from the point P to the wire will be the shortest distance.
So, the bar magnet will experience a force along the line of shortest distance.
A negative charge is given to a nonconducting loop and the loop is rotated in the plane of paper about its centre as shown in figure. The magnetic field produced by the ring affects a small magnet placed above the ring in the same plane :
Figure shown plane figure made of a conductor located in a magnetic field along the inward normal to the plane of the figure. The magnetic field starts diminishing. Then the induced current
As the field diminishes the current is induced in the coils such that if opposes the diminishing of the field. Hence, current is induced in clockwise directing in both the loops.
And as the loops are closed no current will come out of the loops and no current at point R.
Hence option A C D is the correct option.
A conducting wire frame is placed in a magnetic field which is directed into the paper. The magnetic field is increasing at a constant rate. The directions of induced currents in wires AB and CD are
Consider the surface facing upwards having points A, B, C and D in anticlockwise direction when viewing towards the surface from above. Let this be S
flux = S×B
As the flux increases, by Lenz's Law the induced current will be in the direction C B A D C, so as to oppose the increase in flux.
A bar magnet is moved along the axis of copper ring placed far away from the magnet. Looking from the side of the magnet, an anticlockwise current is found to be induced in the ring. Which of the following may be true?
When magnet is moving towards the ring, as the current flows in anti-clockwise direction when seen from magnet, a magnetic field directed towards the magnet from the ring is observed.
By Lenz's law this field is to oppose the movement of the magnet towards the ring.
Therefore the N-pole should be facing the ring, as only then will the induced field by the ring will oppose the movement of the approaching magnet.
Therefore, the north pole faces the ring and the magnet moves towards it and the south pole faces the ring and the magnet moves away from it.
Two circular coils P & Q are fixed coaxially & carry currents I1 and I2 respectively
Which of the following quantities can be written in SI units in K gm2 A-2 S-3 ?
The dimensional formula of a given unit is [ML2T−3A−2].
So, from the given option only resistance has this dimensional formula so resistance is the correct answer.
AB and CD are smooth parallel rails, separated by a distance l, and inclined to the horizontal at an angle q. A uniform magnetic field of magnitude B, directed vertically upwards, exists in the region. EF is a conductor of mass m, carrying a current i. For EF to be in equilibrium,
Force on EF,
Fmag=i∫(dl×B)=iLBsin(90−θ)=iLBcosθ
Fmag up the inclined plane.
Component of weight of EF down the inclined plane: mgsinθ
For EF to be in equilibrium, iLBcosθ=mgsinθ
∴iLB=mgtanθ
For Fmag to be up the inclined plane, it needs to flow from E to F.
AB and CD are smooth parallel rails, separated by a distance l, and inclined to the horizontal at an angle q. A uniform magnetic field of magnitude B, directed vertically upwards, exists in the region. EF is a conductor of mass m, carrying a current i. if B is normal to the plane of the rails
As seen from the image, in the direction of magnetic field
mgsinθ=il×B
mgsinθ=ilB
A conducting rod PQ of length L = 1.0 m is moving with a uniform speed v = 20 m/s in a uniform magnetic field B = 4.0 T directed into the paper. A capacitor of capacity C = 10 mF is connected as shown in figure. Then
According to Fleming’s right-hand rule induced current flows from Q to P.
Hence P is at higher potential and Q is at lower potential.
Therefore, A is positively charged and B is negatively charged.
Hence:
qA=+800μC and qb=−800μC
two different arrangements in which two square wire frames of same resistance are placed in a uniform constantly decreasing magnetic field B.
The value of magnetic flux in each case is given by
f=BA, area of square=(side)2
so, for case I.
loops is continuous,
so, flux should be added,
f=(L2+l2)B
for case II
loop is opposite,
so, flux should be subtracted
f=(L2-l2)B
Two different arrangements in which two square wire frames of same resistance are placed in a uniform constantly decreasing magnetic field B.
The direction of induced current in the case I is
Two different arrangements in which two square wire frames of same resistance are placed in a uniform constantly decreasing magnetic field B.
The direction of induced current in the case II is
Two different arrangements in which two square wire frames of same resistance are placed in a uniform constantly decreasing magnetic field B.
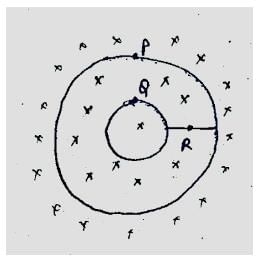
A conducting ring of radius a is rotated about a point O on its periphery as shown in the figure in a plane perpendicular to uniform magnetic field B which exists everywhere. The rotational velocity is w.
Choose the correct statement(s) related to the potential of the points P, Q and R
A conducting ring of radius a is rotated about a point O on its periphery as shown in the figure in a plane perpendicular to uniform magnetic field B which exists everywhere. The rotational velocity is w.
A conducting ring of radius a is rotated about a point O on its periphery as shown in the figure in a plane perpendicular to uniform magnetic field B which exists everywhere. The rotational velocity is w.
Choose the correct statement(s) related to the induced current in ring
In the given question neither the magnetic field nor the area of the ring is changing. So there will be a constant flux in the ring and hence there will be no EMF (or) current induced in the ring.
The horizontal component of the earth's magnetic field at a place is 3 × 10-4 T and the dip is tan-1(4/3). A metal rod of length 0.25 m placed in the north-south position is moved at a constant speed of 10 cm/s towards the east. Find the e.m.f induced in the rod.
A wire forming one cycle of sine curve is moved in x-y plane with velocity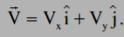 
. There exist a magnetic field 
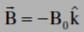. Find the motional emf develop across the ends PQ of wire.
A conducting circular loop is placed in a uniform magnetic field of 0.02 T, with its plane perpendicular to the field. If the radius of the loop starts shrinking at a constant rate of 1.0 mm/s, then find the emf induced in the loop, at the instant when the radius is 4 cm.
Induced EMF E=− (dϕ /dt) , ϕ=A.B, A=πR2
this gives, E=−B (dA /dt) =−πB×2R (dR/dt)
=π×0.02×2×0.04×0.001
=16π×10−7V
Find the dimension of the quantity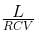 
, where symbols have usual meaning.
We know that:
[V]=[iR]=[L (di/dt) ]
[i][R]= [L][i]/ [t]
Thus, [L/R]=[t]=T
[L]= [V][t]/[i]
Also, i=C (dV/dt) , or [CV]=[i][t]=AT
Thus, [L/RCV]=T/AT=A−1
A rectangular loop with a sliding connector of length l = 1.0 m is situated in a uniform magnetic field B = 2T perpendicular to the plane of loop. Resistance of connector is r = 2W. Two resistances of 6W and 3W are connected as shown in figure. Find the external force required to keep the connector moving with a constant velocity v = 2m/s.
6Ω and 3Ω resistors are in parallel and equivalent resistance is 2Ω+2Ω=4Ω.
F=Bil=BL (BLv/Req)
= B2l2v/Req =(22×12×2)/4=2N
|
157 videos|452 docs|213 tests
|
|
Use Code STAYHOME200 and get INR 200 additional OFF
|
Use Coupon Code |
|
157 videos|452 docs|213 tests
|
How to Prepare for NEET
Download free EduRev App
Related content with Test: Electromagnetic Induction - 2
|
|
|
|
Related tests with Test: Electromagnetic Induction - 2
|
|
|
|
|
|
© EduRev
|
Education Revolution
|
Follow Us
|
