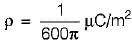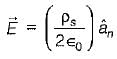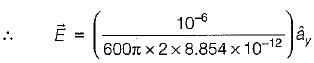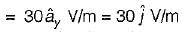Test: Electrostatics- 2 - Electrical Engineering (EE) MCQ
20 Questions MCQ Test - Test: Electrostatics- 2
Which one of the following pairs is NOT correctly matched?
Match List-I (Law/Quantity) with List-ll (Mathematical expression) and select the correct answer using the codes given below the lists:
List-I
A. Gauss’s law
B. Ampere’s law
C. Faraday’s law
D. Poynting vector
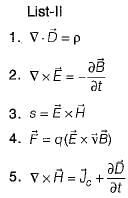
Codes:
A B C D
(a) 1 2 4 3
(b) 3 5 2 1
(c) 1 5 2 3
(d) 3 2 4 1
List-I
A. Gauss’s law
B. Ampere’s law
C. Faraday’s law
D. Poynting vector
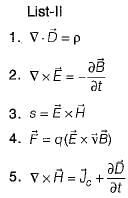
Codes:
A B C D
(a) 1 2 4 3
(b) 3 5 2 1
(c) 1 5 2 3
(d) 3 2 4 1
What is the value of total electric flux coming out of a closed surface?
Which one of the following is the Poisson's equation for a linear and isotropic but in homogeneous medium?
Two concentric spherical shells carry equal and opposite uniformly distributed charges over their surfaces as shown in figure below.

Electric field on the surface of inner shell will be
Electric field intensity due to line charge of infinite length is
Consider the following statements associated with equipotential surface:
1. Potential is same everywhere.
2. No current flows on this surface.
3. Work done in moving charge from one point to another is zero.
4. Potential is different everywhere.
Which of the above statements is/are not correct?
A finite sheet 0 ≤ x ≤ 1, 0 ≤ 1 on the z = 0 plane has a charge density
ρs = xy (x2 + y2 + 25)3/2 nC/m2.
The total charge on the sheet would be
Assertion (A): Gauss’s law is an alternative statement of Coulomb’s law.
Reason (R): Proper application of the divergence theorem to Coulomb’s law results in Gauss’s law.
If the potential V = 10/r2 sinθcosϕ then the work done in moving a 10 μC charge from point A(1, 30°, 120°) to B(4, 90°, 60°) would be equal to
A wire of diameter 1 mm and conductivity 5 x 107S/m has 1029 free electrons /m3 when an electric field of 10 mV/m is applied.
The current density and the drift velocity of the electrons will be respectively given by (take charge on an electrons e = -1.6 x 10-19 C)
Three point charges -1 nC, 4 nC and 3 nC are located at (0, 0, 0) , (0,0,1) and (1,0,0,) respectively. To total energy contained in the system would be
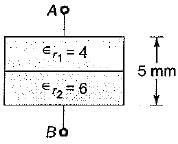
The equivalent capacitance between the terminals A and B for the capacitor shown below would be (the area occupied by each dielectric is 30 cm2)
Match List-I with List-ll and select the correct answer using the codes given below the lists:
List-I
A. Joule’s law
B. Ohm’s law
C. Solenoidal current
D. Continuity equation
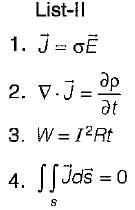
Codes:
A B C D
(a) 4 2 3 1
(b) 3 1 2 4
(c) 3 1 4 2
(d) 4 3 1 2
Assertion (A): An electric field produces no migration of charge in a dieiectric.
Reason (R): The permittivity of a dielectric is always less than the permittivity of vaccum.
The potential field at any point in space containing a dielectric material of relative permittivity 3 is given by V = (5x2y + 3yz2 + 6xz) Volts, where x, y, z are in meters. The magnitude of volume charge density at point (1,2, 3) will be given by
If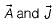 are the vector potential and current density vectors associated with a coil, then
are the vector potential and current density vectors associated with a coil, then 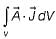 has the unit of
has the unit of
In the infinite plane, y = 6 m, there exists a uniform surface charge density of (1/600π) μC/m2 . The associated electric field strength is


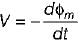

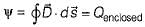 .
.
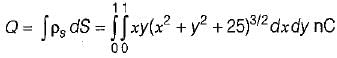
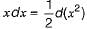 , we now integrate w.r.t. x
, we now integrate w.r.t. x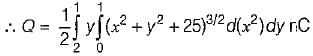
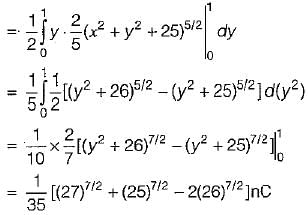

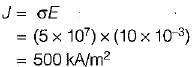

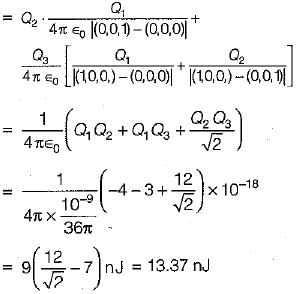
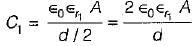
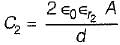

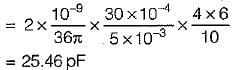
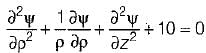
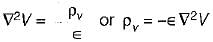

 with electrical energy stored i.e.
with electrical energy stored i.e.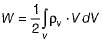 we can find that Wm has the unit of energy.
we can find that Wm has the unit of energy.