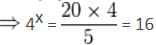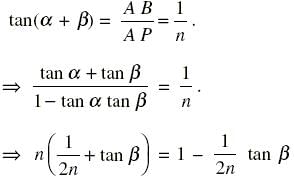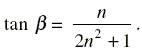Test: Elementary Mathematics - 4 - CDS MCQ
30 Questions MCQ Test CDS (Combined Defence Services) Mock Test Series 2024 - Test: Elementary Mathematics - 4
Which of the following cannot be the factor of both ab and ba if ab is a two-digit number and a, b ≠ 0 and a ≠ b?
What are the respective values of x and y, if the median of the given data is 68 and the total frequency is 22?

| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
What is the ratio of the number of female candidates who appeared for the test from state B to the number of female candidates who appeared for the test from state C?
Directions: A solid consists of a cuboid having length and breadth each equal to 'l' m and the height of the cuboid is 3.14l m. This cuboid is surmounted on a cubical solid of side 'l' m.
What would be volume of the whole solid?
The sum of interior angles of a regular polygon is 1080º. How many sides does the polygon have?
A circus tent is in the form of a cone over a cylinder. The diameter of the base is 6 m, the height of the cylindrical part is 15 m and the total height of the tent is 19 m. The canvas required for the tent is
A 225 m long train is running at a speed of 30 km/hr. How much time does it take to cross a man running at 3 km/hr in the same direction?
A is the smallest integer which when multiplied by 3 gives a number made of 5's only. What is the value of C3, if sum of the digits of A is B and sum of the digits of B is C?
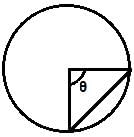
Directions: There is a circular field with radius 6.9 cm and length of its chord is 9.75 cm.
Find the appoximate angle that the chord subtends at centre of the circle.
The interior angles of a convex polygon are in AP. The smallest angle is 120° and the common difference is 5°. Find the number of sides of the polygon.
A small company pays each of its 5 category 'C' workers Rs. 20,000, each of its 3 category 'B' workers Rs. 25,000 and a category 'A' worker Rs. 65,000. The number of workers earning less than the mean salary is
Two equal sums are lent at the same time at 9% and 8% simple interest. The former is recovered 6 months earlier than the latter and the amount in each case is Rs. 17,680. Find the period (in years) for which they are lent.
Ram buys 4 chairs and 9 stools for Rs. 1340. If he sells chairs at 10% profit and stools at 20% profit, he earns a total profit of Rs. 188. How much money did he have to pay for the chairs?
Number of women visiting shopping mall O forms what percent of number of women visiting shopping mall R (approximately)?
Evaluate  + 3 cos 40° cosec 50° - 2 sec 35° sin 55°.
+ 3 cos 40° cosec 50° - 2 sec 35° sin 55°.
How many co-primes of 21 are less than 21 and greater than 1?
The median of a grouped data is 39.8. The lower limit of the median class is 35 and the frequency is 10. The cumulative frequency of the preceding class of the median class is 34 and the total number of observations is 80. The class size of the grouped data is
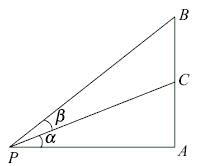
AB is a vertical pole. The end A is on the level ground and C is the middle point of AB. P is a point on the level ground. The portion BC subtends an angle β at P. If AP = nAB, then tan β equals
What is the respective ratio of women visiting shopping mall M to those visiting shopping mall O?
Which one of the following is a correct statement?
A spherical ball of radius 4 cm is to be divided into eight equal pieces by cutting it along the axes, as shown below. Find the surface area of each piece (in cm2).

|
23 docs|73 tests
|
|
23 docs|73 tests
|



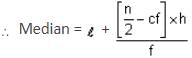
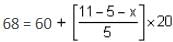
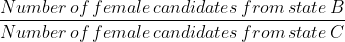
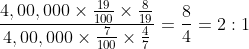

 = 5
= 5 = 30 seconds
= 30 seconds

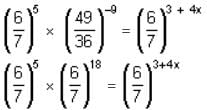
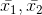 and
and 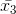 are the means (average) of n1, n2 and n3 observations, respectively, then the combined mean (average) is
are the means (average) of n1, n2 and n3 observations, respectively, then the combined mean (average) is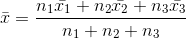
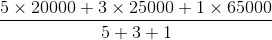
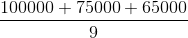
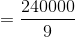
 =
= 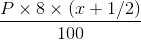
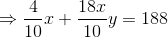
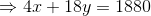 ... (ii)
... (ii) + 3 cos 40° cosec 50° - 2 sec 35° sin 55°
+ 3 cos 40° cosec 50° - 2 sec 35° sin 55° + 3 cos 40° cosec (90° - 40°) - 2
+ 3 cos 40° cosec (90° - 40°) - 2 
 + 3 cos 40° sec 40° -
+ 3 cos 40° sec 40° - 
 1 - 2
1 - 2 

 +
+