Test: Energy & Power
10 Questions MCQ Test Physics Class 11 | Test: Energy & Power
| 1 Crore+ students have signed up on EduRev. Have you? |
How should the force applied on a body be varied with velocity to keep the power of force constant?
We know that power (P) = force (F) x velocity (v).
Since the body is moving with acceleration,v changes and as a result of that P also changes,F being constant.
For P to be constant, F v = constant or F ∝ 1/v i.e
Force should be inversely proportional to the velocity of the body.
Thus,as v increases, F should decrease to keep P constant.
An engine generates a power of 10 kW. In how much time will it raise a mass of 200 kg through a height of 40m.
Power = work done / time
work = force x distance
so power = (force x distance) / time
time = (force x distance) / power
= (2000 N x 40m) / 10000W = 8 seconds
A person 'A' pushes a body of 5 kg placed on a rough surface of co-efficient of friction 0.3 by a distance of 4 m in 15 seconds. Another person 'B' pushes the body of 7 kg on same surface by a distance of 3 m in the same time. Who has more energy and power?
For person A,
Mass of body, m1 = 5kg
Coefficient of friction, μ =0.3
So, The force of friction,
F1= μm1g=0.3 X 5 X 10=15N
Displacement, S1=4m
Therefore,
Work done, W1=15X4=60J
Time taken, t1=15sec
So, Power, P1=60/15=4W
For Person B
Mass of body, m2=7kg
Coefficient of friction, μ =0.3
So, The force of friction,
F1= μm2g=0.3 X 7 X 10=21N
Displacement, S2=3m
Therefore,
Work done, W2=21X3=63J
Time taken, t2=15sec
So, Power, P3=63/15=4.2W
So person B has more energy and power.
A body moves under a force such that momentum of the body at any instant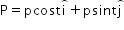 
. What is the rate of work done by the force?
P = p Cos(t) i + p Sin(t) j
dP/dt = -p Sin(t) j + p Cos(t) i
Work done, W = P2/2m
Rate of work done = d/dt(P2/2m)
= 2P/2m x dP/dt
= P/m x dP/dt
= -p2.Sin(t).Cos(t) + p2.Sin(t).Cos(t)
=> Rate of work done = 0
A man A of mass 80 kg runs up a staircase in 12 seconds. Another man of mass 60 kg runs up the same staircase in 11 seconds. The ratio of powers of A and B is :
According to question, 60 kg man runs up a staircase in 12 sec.
m₁ = 80 kg
t₁ = 12 sec
=> A 50 kg man runs up the same staircase in 11 sec:
m₂ = 60 kg
t₂ = 11 sec
=> Rate of work done is equals to power.
∴ P = E/ t and E = mgh
∴ P₁ = m₁gh / t₁
P₂ = m₂gh/ t₂
=> The ratio of Power or Rate of work done is:
P₁/P₂ = m₁gh / t₁ / m₂gh/ t₂
= m₁ * t₂ / m₂ * t₁
= 11 : 9
Thus, the ratio of rate of doing their work is 11 : 9.
If momentum of an object is doubled, how does its kinetic energy change?
As the momentum, P = mv is doubled, we get the new velocity is 2v as mass can’t be increased. Thus if initial KE = ½ mv2
We get new KE = ½ m (2v)2
= 4 times the original one.
An electric motor creates a tension of 4500 N in a hoisting cable and reels it in at the rate of 2 m/s. What is the power of the electric motor?
F=4500N
v=2ms−1
The power of motor is given by
P=F.v
P=45000×2
P=9000W=9kW
From a waterfall, water is falling at the rate of 100 kg/s on the blades of a turbine. If the height of fall is 100 m, the power delivered to the turbine is
Power = work done / time taken
or P = mgh / t
P = (m/t) gh = 100 x 10 x 100 = 100 kW
Calculate the power developed when the force of 10 N is exerted on a body moving with velocity of 3.65 m/s.
Power =F.V
i.e, Power = force x velocity.
here, force (f)= 10N
and velocity (v) = 3.65 m/s
so, Power = f x v,
i.e, 10 x 3.65 = 36.5 w.
A body is moved along a straight line path by a machine delivering constant power. The distance moved by the body in time t is proportional to:
We know that P = F.v
= m.a.a.t
And with u= 0 we have s = ½ at2
Thus we get s = ½ 
Thus as P is constant and m is always the same
we get s is function of t3/2
|
127 videos|464 docs|210 tests
|
|
Use Code STAYHOME200 and get INR 200 additional OFF
|
Use Coupon Code |
|
127 videos|464 docs|210 tests
|
How to Prepare for NEET
Download free EduRev App
Related content with Test: Energy & Power
|
|
|
|
Related tests with Test: Energy & Power
|
|
|
|
|
|
© EduRev
|
Education Revolution
|
Follow Us
|
