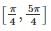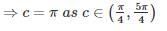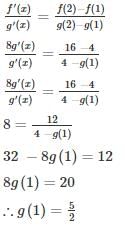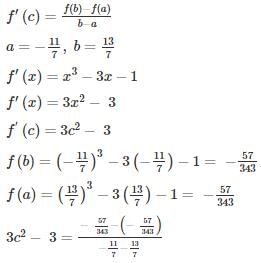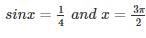Test: Engineering Mathematics- 5 - Computer Science Engineering (CSE) MCQ
10 Questions MCQ Test GATE Computer Science Engineering(CSE) 2025 Mock Test Series - Test: Engineering Mathematics- 5
As xx varies from −1 to +3, which one of the following describes the behaviour of the function f(x) = x3–3x2 + 1?
Given the following statements about a function f : R→R, select the right option:
P: If f(x) is continuous at x = x0, then it is also differentiable at x = x0
Q: If f(x) is continuous at x = x0, then it may not be differentiable at x = x0
R: If f(x) is differentiable at x = x0, then it is also continuous at x = x0
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Given f(x) = x3 + ax2 + bx + c and y-intercept for the function is 1. Also f has local extrema at x = -4 and x = 2. Then a + b + c = ____
Find C of Rolle’s theorem for f(x) = ex(sin x - cos x) in
If f(x) is differentiable and g’(x) ≠ 0 such that f(1) = 4, f(2) = 16, f’(x)= 8g’(x) and g(2) = 4 then what is the value of g(1) ?
An open box is to be made out of square cardboard of 18 cm by cutting offs equal squares from the corners and turning up the sides. What is the maximum volume of the box in cm3?
What are the minimum and maximum value of the below-given function respectively?
f(x) = 3x3 − 9x2 − 27x + 30
Find the point at which maximum value of f(x) = 2x3−3x2 occurs in interval [-2, 2]?
If f(x) = x3 − 3x−1 is continuous in the closed interval 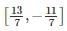 and f’(x) exists in the open interval
and f’(x) exists in the open interval 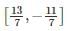 then find the value of c such that it lies in
then find the value of c such that it lies in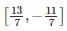
 Find the maximum and minimum values of f(x) = sin x + cos 2x where 0≤ x ≤2π
Find the maximum and minimum values of f(x) = sin x + cos 2x where 0≤ x ≤2π
|
55 docs|215 tests
|
|
55 docs|215 tests
|