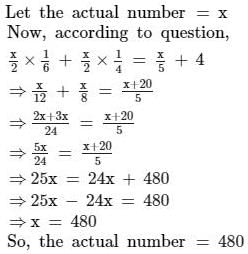Test: Equations- 1 - CA Foundation MCQ
30 Questions MCQ Test - Test: Equations- 1
Choose the most appropriate option (a) (b) (c) or (d)
The equation –7x + 1 = 5–3x will be satisfied for x equal to:
The solution of the equation (p+2) (p–3) + (p+3) (p–4) = p(2p–5) is
The sum of two numbers is 52 and their difference is 2. The numbers are
The diagonal of a rectangle is 5 cm and one of at sides is 4 cm. Its area is
Divide 56 into two parts such that three times the first part exceeds one third of the second by 48. The parts are.
The sum of the digits of a two digit number is 10. If 18 be subtracted from it, the digits in the resulting number will be equal. The number is
The fourth part of a number exceeds the sixth part by 4. The number is
Ten years ago the age of a father was four times of his son. Ten years hence the age of the father will be twice that of his son. The present ages of the father and the son are.
The product of two numbers is 3200 and the quotient when the larger number is divided by the smaller is 2.The numbers are
The denominator of a fraction exceeds the numerator by 2. If 5 be added to the numerator the fraction increases by unity. The fraction is.
Three persons Mr. Roy, Mr. Paul and Mr. Singh together have Rs. 51. Mr. Paul has Rs. 4 less than Mr. Roy and Mr. Singh has got Rs. 5 less than Mr. Roy. They have the money as.
A number consists of two digits. The digits in the ten’s place is 3 times the digit in the unit’s place. If 54 is subtracted from the number the digits are reversed. The number is
One student is asked to divide a half of a number by 6 and other half by 4 and then to add the two quantities. Instead of doing so the student divides the given number by 5. If the answer is 4 short of the correct answer then the actual answer is
If a number of which the half is greater than 1/5th of the number by 15 then the number is
The solution of the set of equations 3x + 4y = 7, 4x – y = 3 is
The values of x and y satisfying the equations are given by the pair.
Solve for x and y : x–3y =0, x+2y = 20. The values of x and y are given as
The simultaneous equations 7x–3y = 31, 9x–5y = 41 have solutions given by