Test: Equations- 3 - CA Foundation MCQ
30 Questions MCQ Test - Test: Equations- 3
A man went to the Reserve Bank of India with Rs. 1, 000. He asked the cashier to give him Rs. 5 and Rs.10 notes only in return. The man got 175 notes in all. Find how many notes of Rs. 5 and Rs. 10 did he receive?
The area of a triangle with vertices (1,3), (5, 6) and (-3, 4) in terms of square units is:
The equation of the straight line through the point of intersection of x+2y-5=0 and x-3y-7=0 and passing through the point (1, 0) is :
A man starts his job with a certain monthly salary and earns a fixed increment every year. If his salary was Rs. 1,500 after 4 years of service and Rs. 1,800 after 10 years of service, what was his starting salary and what is the annual increment in rupees?
The equation of the straight line through the point of intersection of x+2y-5=0 and x-3y-7=0 and passing through the point (1, 0) is :
Find the positive value of k for which the equations: x2+kx+64=0 and x2-8x+k=0 will have real roots
The value of k for which the points (k,1), (5, 5) and (10,7) may be collinear is:
A man sells 6 radios and 4 televisions for Rs. 18,480. If 14 radios and 2 televisions are sold for the same amount, what is the price of a televisions?
The value of k for which the points (k,1), (5, 5) and (10,7) may be collinear is:
The centroid of the triangle ABC is at the point (2,3). A and B are the points (5, 6) and (-1, 4) respectively. The coordinates of C are:
The line joining (-1,1) and (2,-2) and the line joining (1,2) and (2, k) are perpendicular to each other for the following value of k:
A man sells 6 radios and 4 televisions for Rs. 18,480. If 14 radios and 2 televisions are sold for the same amount, what is the price of a televisions?
A man went to the Reserve Bank of India with Rs. 1, 000. He asked the cashier to give him Rs. 5 and Rs.10 notes only in return. The man got 175 notes in all. Find how many notes of Rs. 5 and Rs. 10 did he receive?
Root of the equation 3x2-14x+k=0 will be reciprocal of each other if:
If (2+√3)is a root of a quadratic equation x2+px+q=0 then find the value of p and q.
Calculate the length of the diagonal of a square sheet if its sides are 4 cm each.
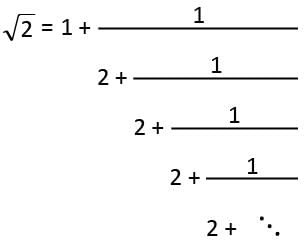
One root of the equation:
X2-2(5+m)x+3(7+m)=0 is reciprocal of the other.
Find the value of M.
If area and perimeter of a rectangle is 6000 cm2 and 340 cm respectively, then the length of rectangle is:
Find the equation of the line joining the point (3, 5) with the point of intersection 2x+3y-5=0 and 3x+5y-7=0.
A straight line passes through the point (3, 2). Find the equation of the straight line.
If the length of a rectangle is 5 cm more than the breadth and if the perimeter of the rectangle is 40cm, then the length & breadth of the rectangle with be:
A man rowing at the rate of 5km in an hour in still water takes thrice as much time in going 40km up the river as in going 40km down. Find the rate at which the river flows:
Find the equation of the line passing through the point (1, 1) and parallel to the line 3x+5y+17=0
The sum of two numbers is 52 and their difference is 2. The numbers are



















