Test: Equilibrium In Three Dimensions - Mechanical Engineering MCQ
15 Questions MCQ Test - Test: Equilibrium In Three Dimensions
A force is developed by a support that not allows the ________ of its attached member.
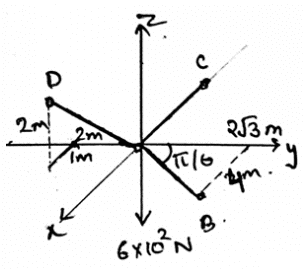
In the diagram given below, coordinates of D is (1, -2, 2), C (-2, 0, 0) and B are as shown. The dark region is the cables holding the weight of 600N at origin. Find the tension in the AD section.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A couple moment is developed when _______ of the attached member is prevented.
What is not the condition for the equilibrium in three dimensional system of axis?
We first make equilibrium equations of the body by considering all the three dimensional forces and then the free body diagram is made and solved.
If solving the question in 3D calculations is difficult, then use the 2D system and then equate the total net force to zero.
∑Fx=0, ∑Fy=0 and ∑Fz=0 are vector equations for the three dimensions. They are satisfied when the body is achieved it state of equilibrium.
If the resolved force or the force which you get as the answer after solving the question is negative, then what does this implies?
The supports in the 3D are having more than three reaction forces. Because they are having three axis on which the components of the forces need to be zero.
If any body is tied to three or more ropes, and then is allowed to achieve its equilibrium. Then the equilibrium achieved is achieved w.r.t what?
The single pin, single bearing and single hinge resist _______
If the supports are properly aligned then the reaction forces developed are adequate to support the body.
Determine the value of the q, parallel to the z axis. That is the point of intersection of the projections of the points A, B and C parallel to the xy plane. With the distance between the tri-section point and the points A, B and C be equal to 0.6m.
If the supports are not properly aligned then the reaction forces developed are adequate to support the body.

















