Statement 1 says “x times z is odd.” That immediately tells us the answer is “yes” (an odd product means xz is odd).
Statement 2 says x = 2y That only tells us x is a power of 2 (so either 1 if y=0, or an even number if y≥1). Without knowing z, we can’t tell if xz is odd or even (for example, if x=2 and z=1, xz=2 is even; if x=1 and z=any number, xz=z could be odd or even).
Therefore exactly one statement suffices.
Answer: (a) Exactly one of the statements can answer the question.




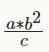 = even > 0 ab2 = c* even = even--> either a is even or b or both.
= even > 0 ab2 = c* even = even--> either a is even or b or both.










