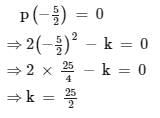Test: Factorisation Factor Theorem - Class 9 MCQ
20 Questions MCQ Test Online MCQ Tests for Class 9 - Test: Factorisation Factor Theorem
x-a is a factor of p(x) = ax2+bx+c. Which of the following is true?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If (x-2) is the factor of x2 + 2x+ a, find the value of ‘a’.
If a polynomial p(x) is divided by a linear divisor (x-a), then the remainder is
The value of p for which x + p is a factor of x2 + px + 3 – p is:
For two polynomials p(x) and q(x), x-a and x-b are their factors, respectively.Which of the following is true?
Find the value of a such that (x – 2) is the factor of the polynomial x4 + ax3 + 2x2– 3x
What is the value of b such that x+3 is a factor of x2 - bx -12?
Find the value of ‘a’ so that (x-1) is the factor of x2+a+1
For a polynomial p(x), x-2 is a factor, so p(2) is _______
x+1 is a factor of p(x) = x3+3x2+3x+1, so what is the value of p(-1)
If (x-1) is a factor of ax – a, then find the value of a
For a polynomial p(x), p(-1) and p(2) are both equal to zero .So, we can conclude that,
For a polynomial, x2 – 3x +2, which of the following is a factor ?
If (2x + 5) is a factor of 2x2 – k, then the value of k is.
(x + 2) is a factor of 2x3 + 5x2 - x - k. The value of k is:
If x-2 is a factor of ax2-x-6, so what should be the value of a?
Find the value of p(2) if p(x) has (x-2) as its factor
Which of the following polynomials has -3 as a zero?
|
5 docs|319 tests
|