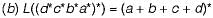Test: Finite Automata: Regular Languages- 1 - Computer Science Engineering (CSE) MCQ
9 Questions MCQ Test Question Bank for GATE Computer Science Engineering - Test: Finite Automata: Regular Languages- 1
Let r1 = ab*c*and r2 = (a*b+c)*and r3 = (a+b+c)*. Then which of the following is true
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Let ∑ = {a, b}, r1 = a(a + b)* and r2 = b(a + b)*. Which of the following is true?
Which of the following statements are true?
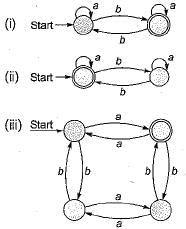
(i) abcd ∈ L((b*a*)* (d*c*)*)
(ii) abcd ∈ L((d*c*b*a*)*)
(iii) abcd ∈ L((a*b*a*c*d*)*)
Which of the following are regular languages?
(i) The language 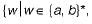 w has an odd number of b’s}.
w has an odd number of b’s}.
(ii) The language 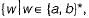 w has an even number of b’s).
w has an even number of b’s).
(iii) The language 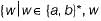 has an even number of b’s and odd number of a’s).
has an even number of b’s and odd number of a’s).
Which of the following regular expression corresponds to the language of all strings over the alphabet {a, b) that contains exactly two a’s
(i) aa
(ii) ab*a
(iii) b* ab*a
Which of the following regular expression corresponds to the language of all strings over the alphabet {a, b} that do not end with ab?
What is regular expression corresponding to the language of strings of even lengths over the alphabet of {a, b}?
How many minimum number of states are required in the DFA (over the alphabet {a, b}) accepting all the strings with the number of a’s divisible by 4 and number of b’s divisible by 5?
|
63 videos|8 docs|165 tests
|
|
63 videos|8 docs|165 tests
|


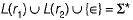
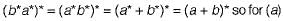
 gives all the combinations of a and b followed by all the combinations of c and d, for
gives all the combinations of a and b followed by all the combinations of c and d, for