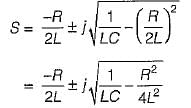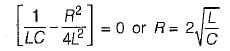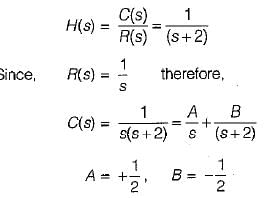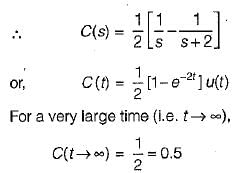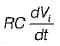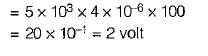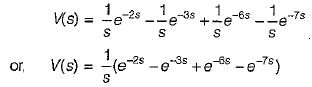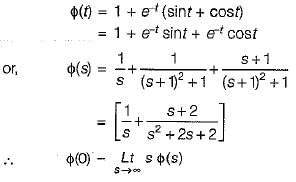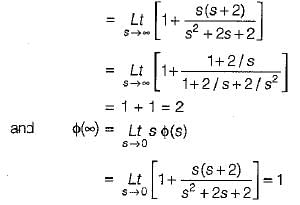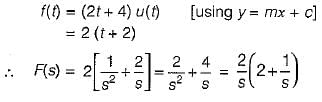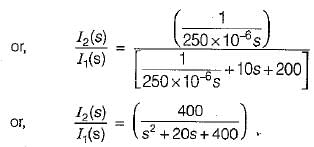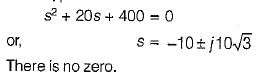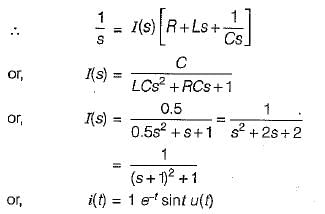Test: First Order RL & RC Circuits - 1 - Electrical Engineering (EE) MCQ
10 Questions MCQ Test - Test: First Order RL & RC Circuits - 1
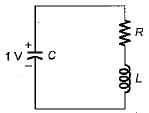
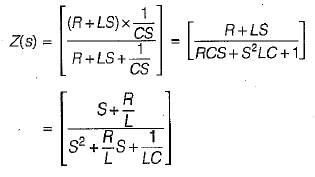
The poles of the impedance Z(s) for the network shown in figure below will be real and coincident if


In the complex frequency S= σ + jω, ω has the unit of radian/sec and σ has the unit of
A system is described by the transfer function 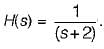 The value of its step response at a very large time will be close to
The value of its step response at a very large time will be close to
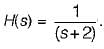 The value of its step response at a very large time will be close to
The value of its step response at a very large time will be close to At a certain current, the energy stored in iron cored coil is 1000 J and its copper loss is 2000 W. The time constant (in second) of the coil is
A ramp voltage vi(t) = 100t V is applied to a differentiator circuit with R = 5 kΩ and C=4μF.The maximum output voltage is
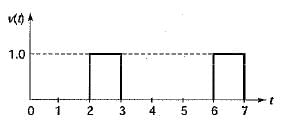
The Laplace transform of the waveform below is
The initial and final values of 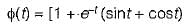 are given by
are given by
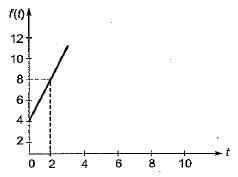
The Laplace transform of the ramp function shown below is
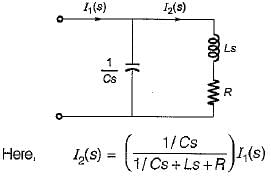
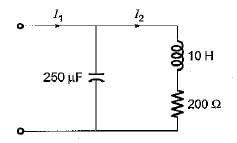
The poles and zeros of the transfer function 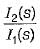 for the circuit shown below are located at
for the circuit shown below are located at
A capacitor of 0.5 F is initially charged to 1 volt and is subjected to discharge at t = 0 across a LR series circuit where 1 = 1 H; R = 2 Ω. The current i(t) for t> 0 is