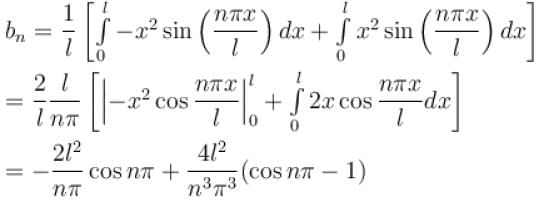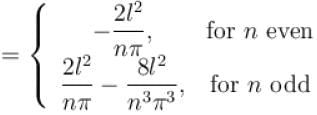Test: Fourier Series- 2 - Electronics and Communication Engineering (ECE) MCQ
10 Questions MCQ Test - Test: Fourier Series- 2
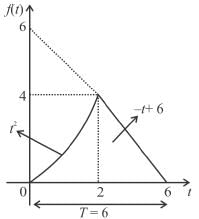
Given the following periodic function, f(t).
f (t) = { t2 for 0 ≤ t ≤ 2 ;
-t + 6 for 2 ≤ t ≤ 6
The coefficient a0 of the continuous Fourier series associated with the above given function f(t) can be computed as
Select one:
-t + 6 for 2 ≤ t ≤ 6

The coefficient a0 of the continuous Fourier series associated with the above given function f(t) can be computed as
Select one:
For the given periodic function 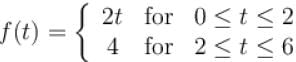 with a period T = 6. The Fourier coefficient a1 can be computed as
with a period T = 6. The Fourier coefficient a1 can be computed as
Select one:
Sum of the series at 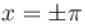 for the periodic function f with period 2π is defined as
for the periodic function f with period 2π is defined as
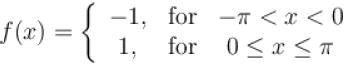
Select one:
Which of the following is an “even” function of t?
Select one:
A “periodic function” is given by a function which
Select one:
For the given periodic function 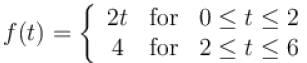 with a period T = 6. The complex form of the Fourier series can be expressed as
with a period T = 6. The complex form of the Fourier series can be expressed as 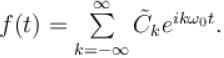 The complex coefficient
The complex coefficient 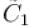 can be expressed as
can be expressed as
Select one:
The function x2 is periodic with period 2l on the interval [–l, l]. The value of an is given by
Select one:
The function x2 extended as an odd function in [–l, l] by redefining it as
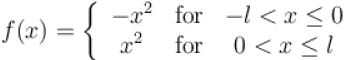
sum of series at x = l.
Select one:


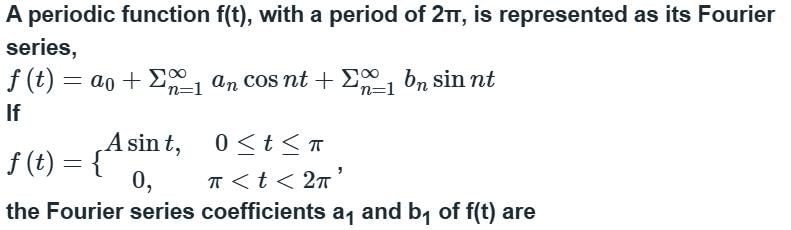
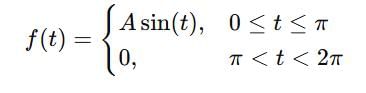
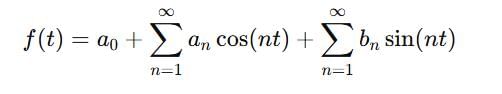
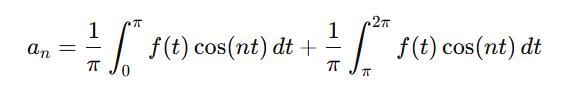

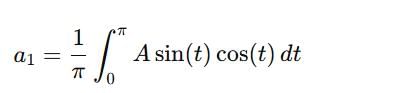
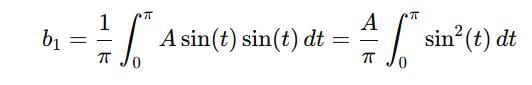
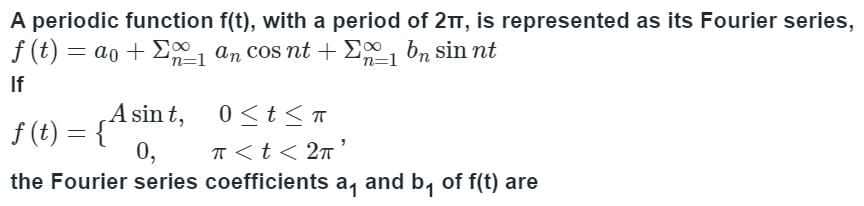


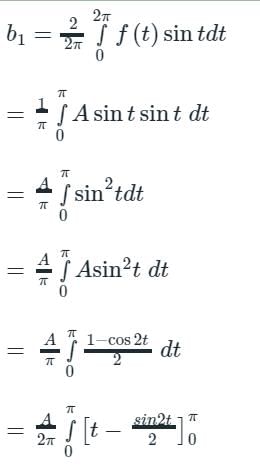


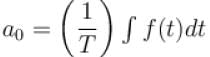
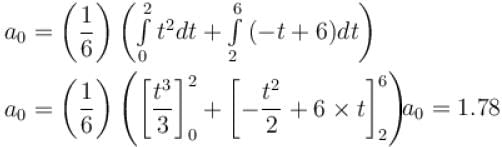
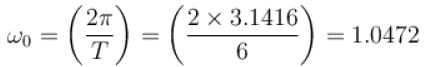
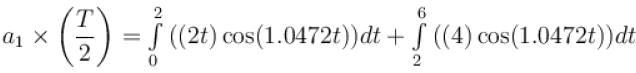
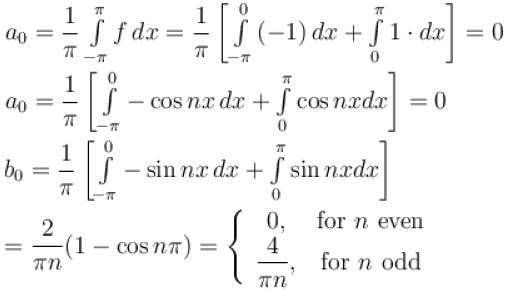
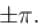
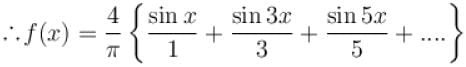

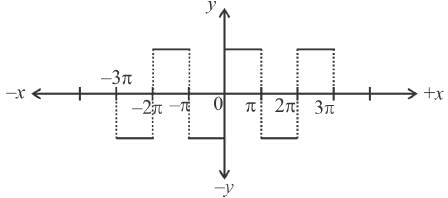
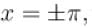 the sum of the series
the sum of the series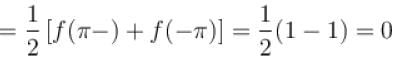
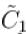 (corresponding to k = 1) can be expressed as :
(corresponding to k = 1) can be expressed as :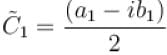
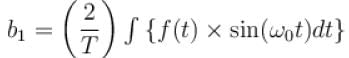

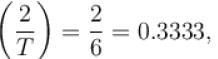
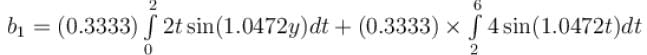
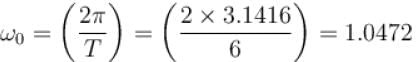
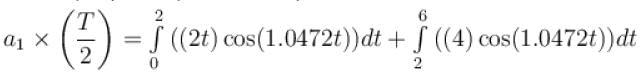
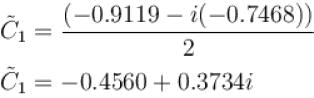
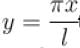 transforms the function into a periodic function with period
transforms the function into a periodic function with period  . Moreover it is an even function.
. Moreover it is an even function.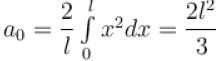
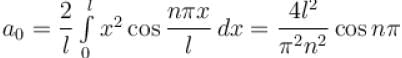
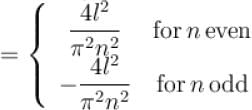
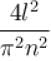 for n even
for n even transforms it into an odd periodic function on [-π, π],
transforms it into an odd periodic function on [-π, π],