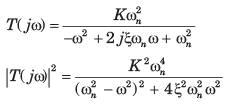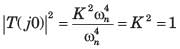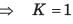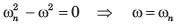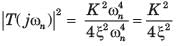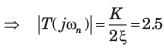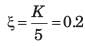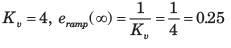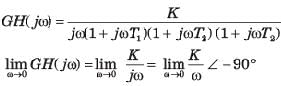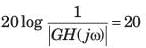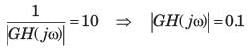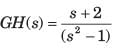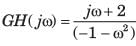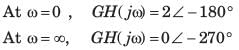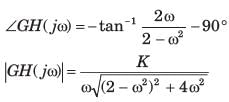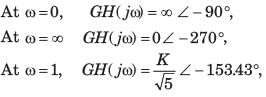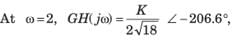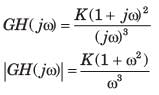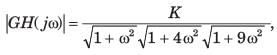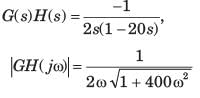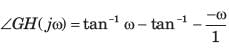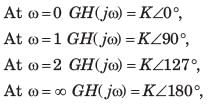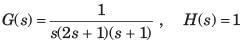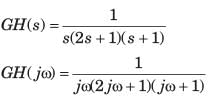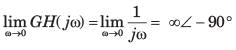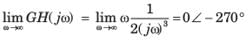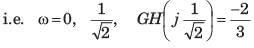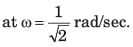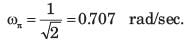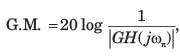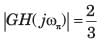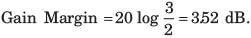Test: Frequency - Domain Analysis - Electronics and Communication Engineering (ECE) MCQ
20 Questions MCQ Test - Test: Frequency - Domain Analysis
An under damped second order system having a transfer function of the form
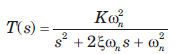
has a frequency response plot shown in fig.
Q. The system gain K is
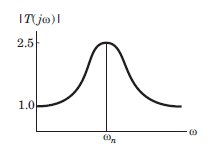
An under damped second order system having a transfer function of the form
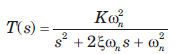
has a frequency response plot shown in fig.

Q. The damping factor ξ is approximately
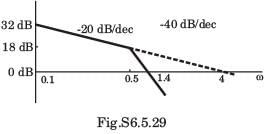
Consider the Bode plot of a ufb system shown in fig.
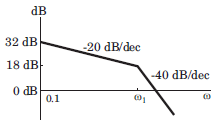
Q. The steady state error corresponding to a rampinput is
Consider the Bode plot of a ufb system shown in fig.
The damping ratio is
The Nyquist plot of a open-loop transfer function G(jω)H(jω) of a system encloses the (-1, j0) point. The gain margin of the system is
Consider a ufb system
The angle of asymptote, which the Nyquist plotapproaches as ω → 0 is
If the gain margin of a certain feedback system isgiven as 20 dB, the Nyquist plot will cross the negativereal axis at the point
The transfer function of an open-loop system is
The Nyquist plot will be of the form
Consider a ufb system whose open-loop transfer function is
The Nyquist plot for this system is
The open loop transfer function of a system is
The Nyquist plot for this system is
For the certain unity feedback system
The Nyquist plot is
The Nyquist plot of a system is shown in fig. The open-loop transfer function is
The no. of poles of closed loop system in RHP are
The open-loop transfer function of a feedback control system is
Q. The Nyquist plot for this system is
If the damping of the system becomes equal to zero, which condition of the resonant frequency is likely to occur?
A unity feedback system has the open loop transfer function G(s)=1/((s−1)(s+2)(s+3))
The Nyquist plot of GG encircle the origin
The open-loop transfer function of a feedback system is
Q. The Nyquist plot of this system is
The open-loop transfer function of a feedback system is
The system is stable for K
A unity feedback system has open-loop transfer function
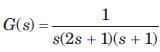
Q. The Nyquist plot for the system is
A unity feedback system has open-loop transfer function
Q. The phase crossover and gain crossover frequenciesare
A unity feedback system has open-loop transfer function
The gain margin and phase margin are