Test: Geometry (March 25) - CAT MCQ
10 Questions MCQ Test Daily Test for CAT Preparation - Test: Geometry (March 25)
A vertical stick 20 m long casts a shadow 10 m long on the ground. At the same time, a tower casts a shadow 50 m long on the ground. Find the height of the tower.
The area of similar triangles, ABC and DEF are 144cm2 and 81 cm2 respectively. If the longest side of the larger △ABC be 36 cm, then the longest side of the smaller △DEF is:
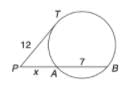
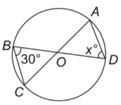
Find the value of x in the figure, if it is given that AC and BD are diameters of the circle.

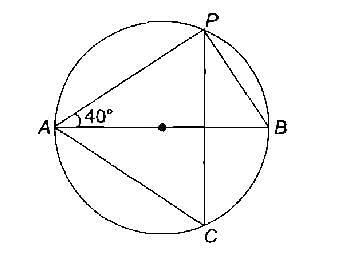
AB is the diameter of the circle and ∠PAB=40∘
what is the value of ∠PCA?
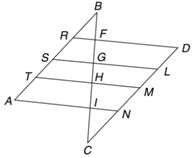
In the figure, AB is parallel to CD and RD || SL || TM || AN, and BR : RS : ST : TA = 3 : 5 : 2 : 7. If it is known that CN = 1.333 BR. Find the ratio of BF : FG : GH : HI : IC
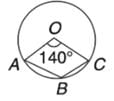
In the following figure, it is given that O is the centre of the circle and ㄥAOC = 140°. Find ㄥABC.
In the figure below, PQ = QS, QR = RS and angle SRQ = 100°. How many degrees is angle QPS?
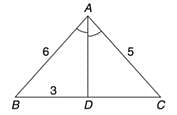
In the given figure, AD is the bisector of ∠BAC, AB = 6 cm, AC = 5 cm and BD = 3 cm. Find DC.
|
152 docs|327 tests
|