Test: Graph - 1 - Computer Science Engineering (CSE) MCQ
15 Questions MCQ Test Programming and Data Structures - Test: Graph - 1
The most efficient algorithm for finding the number of connected components in an undirected graph on n vertices and m edges has time complexity.
Consider an undirected unweighted graph G. Let a breadth-first traversal of G be done starting from a node r. Let d(r, u) and d(r, v) be the lengths of the shortest paths from r to u and v respectively, in G. lf u is visited before v during the breadth-first traversal, which of the following statements is correct?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
How many undirected graphs (not necessarily connected) can be constructed out of a given set V= {V 1, V 2,…V n} of n vertices ?
Which of the following statements is/are TRUE for an undirected graph?
P: Number of odd degree vertices is even
Q: Sum of degrees of all vertices is even
Consider an undirected random graph of eight vertices. The probability that there is an edge between a pair of vertices is 1/2. What is the expected number of unordered cycles of length three?
Given an undirected graph G with V vertices and E edges, the sum of the degrees of all vertices is
What is the maximum number of edges in an acyclic undirected graph with n vertices?
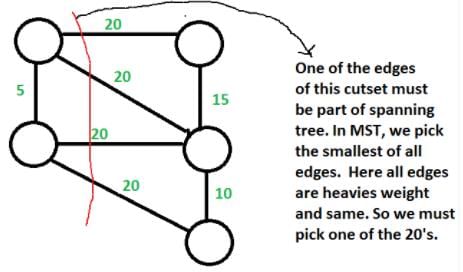
Let G be a weighted undirected graph and e be an edge with maximum weight in G. Suppose there is a minimum weight spanning tree in G containing the edge e. Which of the following statements is always TRUE?
What is the largest integer m such that every simple connected graph with n vertices and n edges contains at least m different spanning trees?
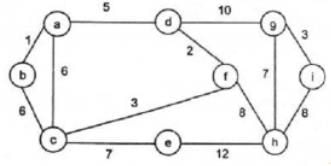
For the undirected, weighted graph given below, which of the following sequences of edges represents a correct execution of Prim’s algorithm to construct a Minimum Spanning Tree?
Let G be a simple graph with 20 vertices and 8 components. If we delete a vertex in G, then number of components in G should lie between ____.
Which of the following data structure is useful in traversing a given graph by breadth first search?
Which kind of traversal order trie gives the lexicographical sorting of the set of the strings?
You are given a graph containing n vertices and m edges and given that the graph doesn’t contain cycle of odd length. Time Complexity of the best known algorithm to find out whether the graph is bipartite or not is ?
|
119 docs|30 tests
|
|
119 docs|30 tests
|