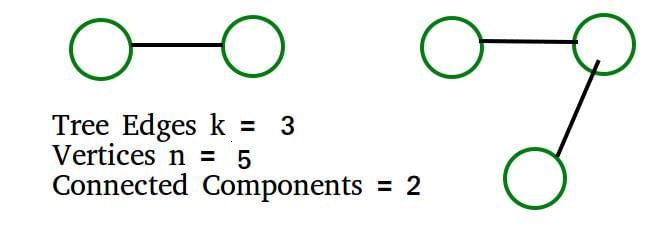Test: Graph Based Algorithms- 2 - Computer Science Engineering (CSE) MCQ
20 Questions MCQ Test Algorithms - Test: Graph Based Algorithms- 2
How many undirected graphs (not necessarily connected) can be constructed out of a given set V = {v1, v2, ... vn} of n vertices?
If the DFS finishing time f[u] > f[v] for two vertices u and v in a directed graph G, and u and v are in the same DFS tree in the DFS forest, then u is an ancestor of v in the depth first tree.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
What is the maximum number of edges in an acyclic undirected graph with n vertices?
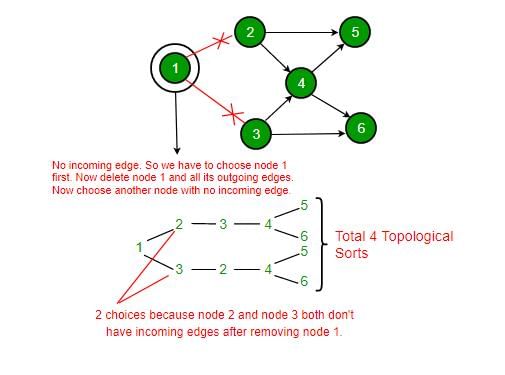
Consider the DAG with Consider V = {1, 2, 3, 4, 5, 6}, shown below. Which of the following is NOT a topological ordering?
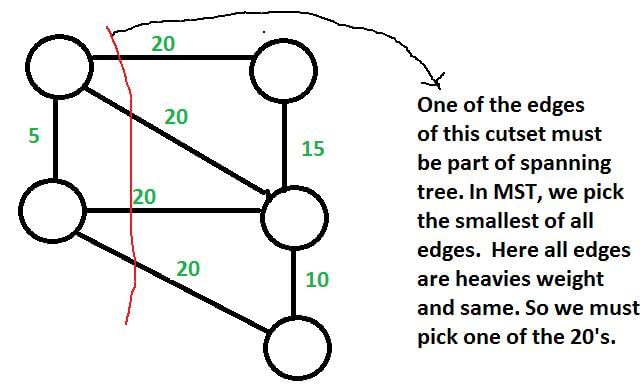
Let G be a weighted undirected graph and e be an edge with maximum weight in G. Suppose there is a minimum weight spanning tree in G containing the edge e. Which of the following statements is always TRUE?
Let G be a graph with n vertices and m edges. What is the tightest upper bound on the running time on Depth First Search of G? Assume that the graph is represented using adjacency matrix.
The cyclomatic complexity of the flow graph of a program provides
Consider the tree arcs of a BFS traversal from a source node W in an unweighted, connected, undirected graph. The tree T formed by the tree arcs is a data structure for computing.
What is the largest integer m such that every simple connected graph with n vertices and n edges contains at least m different spanning trees?
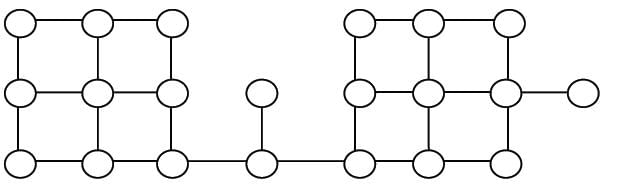
Suppose depth first search is executed on the graph below starting at some unknown vertex. Assume that a recursive call to visit a vertex is made only after first checking that the vertex has not been visited earlier. Then the maximum possible recursion depth (including the initial call) is _________.
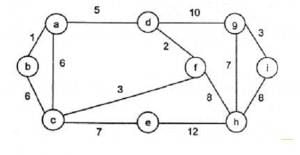
For the undirected, weighted graph given below, which of the following sequences of edges represents a correct execution of Prim's algorithm to construct a Minimum Spanning Tree?
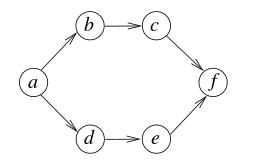
Let T be a depth first search tree in an undirected graph G. Vertices u and n are leaves of this tree T. The degrees of both u and n in G are at least 2. which one of the following statements is true?
Consider a directed graph with n vertices and m edges such that all edges have same edge weights. Find the complexity of the best known algorithm to compute the minimum spanning tree of the graph?
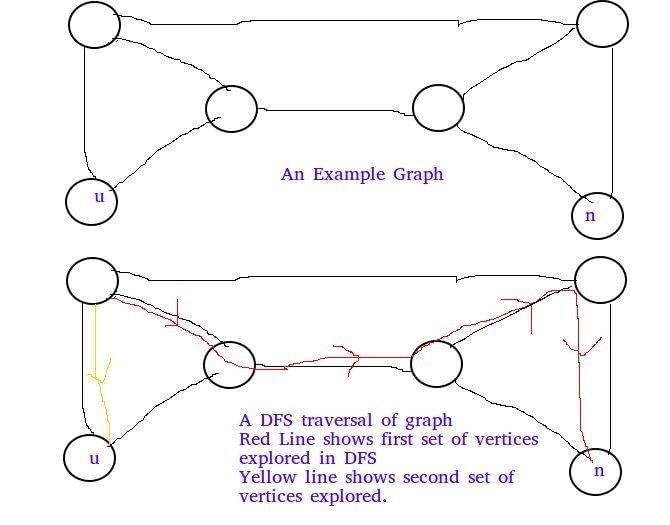
Let G be an undirected graph. Consider a depth-first traversal of G, and let T be the resulting depth-first search tree. Let u be a vertex in G and let v be the first new (unvisited) vertex visited after visiting u in the traversal. Which of the following statements is always true?
You are given a graph containing n vertices and m edges and given that the graph doesn’t contain cycle of odd length. Time Complexity of the best known algorithm to find out whether the graph is bipartite or not is ?
In a depth-first traversal of a graph G with n vertices, k edges are marked as tree edges. The number of connected components in G is
Let G be a simple graph with 20 vertices and 8 components. If we delete a vertex in G, then number of components in G should lie between ____.
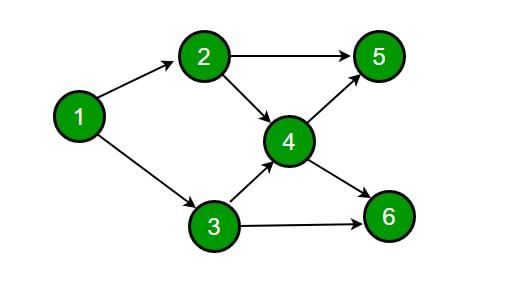
Consider the following directed graph.
The number of different topological orderings of the vertices of the graph is Note : This question was asked as Numerical Answer Type.
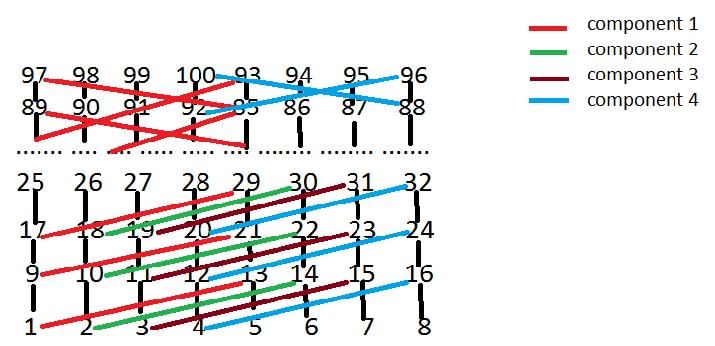
Let G be the graph with 100 vertices numbered 1 to 100. Two vertices i and j are adjacent iff |i−j|=8 or |i−j|=12. The number of connected components in G is
Let G = (V, G) be a weighted undirected graph and let T be a Minimum Spanning Tree (MST) of G maintained using adjacency lists. Suppose a new weighed edge (u, v) ∈ V×V is added to G. The worst case time complexity of determining if T is still an MST of the resultant graph is
|
81 videos|80 docs|33 tests
|
|
81 videos|80 docs|33 tests
|