Test: Graphs Algorithms- 1 - Computer Science Engineering (CSE) MCQ
15 Questions MCQ Test GATE Computer Science Engineering(CSE) 2025 Mock Test Series - Test: Graphs Algorithms- 1
Consider the directed graph shown in the figure below. There are multiple shortest paths between vertices and . Which one will be reported by Dijkstra’s shortest path algorithm? Assume that, in any iteration, the shortest path to a vertex is updated only when a strictly shorter path to is discovered.
Let G be a graph with n vertices and m edges. What is the tightest upper bound on the running time on Depth First Search of G? Assume that the graph is represented using adjacency matrix.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
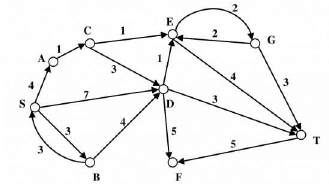
What is the time complexity of Bellman-Ford single-source shortest path algorithm on a complete graph of n vertices?
Consider the directed graph below given.
Which one of the following is TRUE?
Consider the tree arcs of a BFS traversal from a source node W in an unweighted, connected, undirected graph. The tree T formed by the tree arcs is a data structure for computing
be a simple undirected graph, and be a particular vertex in it called the source.
denote the shortest distance in G from s to x. A breadth first search (BFS) is performed starting at s. Let T be the resultant BFS tree. If (u,v) is an edge of G that is not in Tthen which one of the following CANNOT be the value of ,
In an adjacency list representation of an undirected simple graph G = (V,E) , each edge (u,v) has two adjacency list entries: [v] in the adjacency list of u , and [u] in the adjacency list of v. These are called twins of each other. A twin pointer is a pointer from an adjacency list entry to its twin. If , and the memory size is not a constraint, what is the time complexity of the most efficient algorithm to set the twin pointer in each entry in each adjacency list?
Let G = (V,E) be connected undirected edge-weighted graph. The weights of the edges in E are positive and distinct. Consider the following statements:
(I) Minimum Spanning Tree of G is always unique.
(II) Shortest path between any two vertices of G is always unique.
Which of the above statements is/are necessarily true?
The Breadth First Search (BFS) algorithm has been implemented using the queue data structure. Which one of the following is a possible order of visiting the nodes in the graph below?
Let G be an undirected graph. Consider a depth-first traversal of G, and let T be the resulting depth-first search tree. Let u be a vertex in G and let v be the first new (unvisited) vertex visited after visiting u in the traversal. Which of the following statement is always true?
Consider the following directed graph.
Suppose a depth-first traversal of this graph is performed, assuming that whenever there is a choice, the vertex earlier in the alphabetical order is to be chosen. Suppose the number of tree edges is , the number of back edges is and the number of cross edges is . Then
The minimum number of record movements required to merge five files A (with 10 records), B (with 20 records), C (with 15 records), D (with 5 records) and E (with 25 records) is:
We are given 9 tasks The execution of each task requires one unit of time. We can execute one task at a time. Each task Ti has a profit Pi and a deadline di . Profit Pi is earned if the task is completed before the end of the dith unit of time.
Are all tasks completed in the schedule that gives maximum profit?
We are given 9 tasks The execution of each task requires one unit of time. We can execute one task at a time. Each task Ti has a profit Pi and a deadline di . Profit Pi is earned if the task is completed before the end of the dith unit of time.
What is the maximum profit earned?
For which of the following combinations of the degrees of vertices would the connected graph be eulerian?
|
55 docs|215 tests
|
|
55 docs|215 tests
|

















