Test: Graphs & Hashing- 2 - Computer Science Engineering (CSE) MCQ
10 Questions MCQ Test Question Bank for GATE Computer Science Engineering - Test: Graphs & Hashing- 2
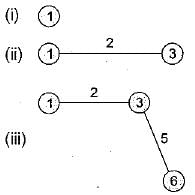
Let M be a 3 x3, adjacency matrix corresponding to a given graph of three nodes labeled 1,2, 3. If entry (1,3) in M3 is 2, then the graph could be
Consider the graph in figure:
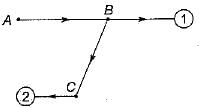
What should be the labels of nodes marked 1 and 2 if the breadth first traversal yields the list a b c d e?

What should be the labels of nodes marked 1 and 2 if the breadth first traversal yields the list a b c d e?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Consider the graph in:
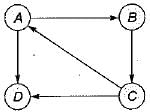
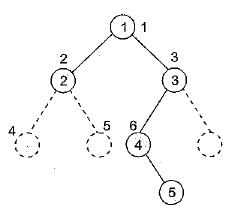
Which of the following is a valid strong component?

Which of the following is a valid strong component?
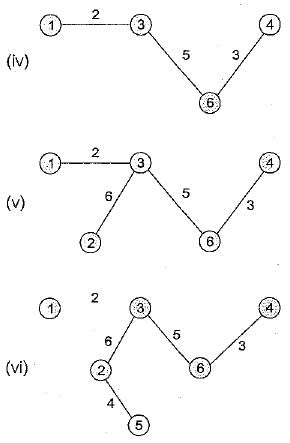
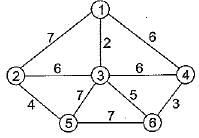
Consider the undirected weighted graph in figure. The minimum cost spanning tree for this graph has the cost.
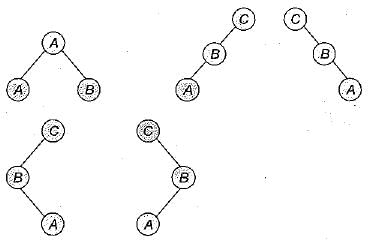
The number of binary trees with 3 nodes which when traversed in post-order gives the sequence A, B, C is
The minimum number of colors needed to color a graph having n (> 3) vertices and 2 edges is
The number of edges in a regular graph of degree d and n vertices is
The number of binary relations on a set with n elements is
How many real links are required to store a sparse matrix of 10 rows, 10 columns, and 15 non-zero entries, (Pick up the closest answer)
|
63 videos|8 docs|165 tests
|
|
63 videos|8 docs|165 tests
|