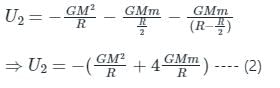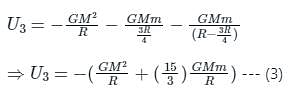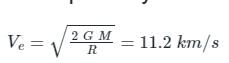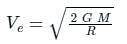Test: Gravitational Potential Energy & Escape Speed (August 11) - NEET MCQ
10 Questions MCQ Test Daily Test for NEET Preparation - Test: Gravitational Potential Energy & Escape Speed (August 11)
The mass of stone A is more than stone B, then the ratio of the escape velocity of stone A to stone B from the surface of the earth is:
Let V and E denote the gravitational potential and gravitational field at a point. Then which of the following is possible at a particular location?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
What is the escape speed on earth for any object?
Gravitational force exists between ________ objects, but it cannot be felt unless the mass of the objects is very high, such as in planets.
The escape velocity on Earth is 11.2 kms-1. What would be the escape velocity on a planet whose mass is 1000 times and whose radius is 10 times that of the earth?
The gravitational potential energy (U) associated with two particles of masses 'm1' and 'm2' and separated by a distance 'r' is given by ________.
The relation between escape velocity (ve) and orbital velocity (v0) on the surface of the earth is
Two identical spherical masses are kept at some distance as shown. Potential energy when a mass m is taken from the surface of one sphere to the other
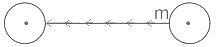
Escape velocity (ve) of a body depends upon its mass (m) as: (Here M is mass of earth)
Which term is used for celestial bodies that revolve around the sun in highly elliptical orbit ?
|
12 docs|366 tests
|


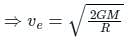

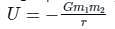
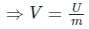
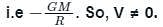
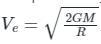
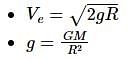
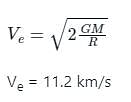
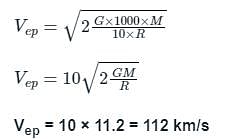
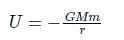
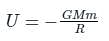
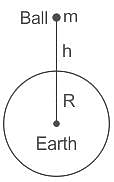
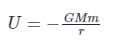
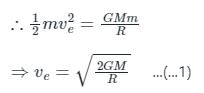
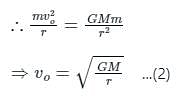
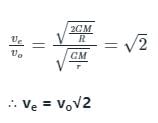
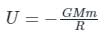

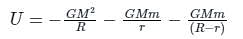
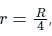 the potential energy of the system is,
the potential energy of the system is,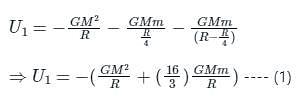
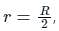 the potential energy of the system is,
the potential energy of the system is,