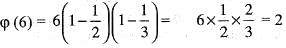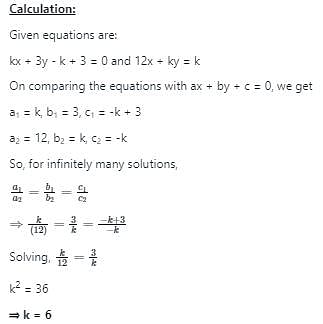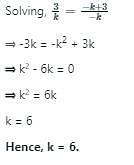Courses
Get the App Signup / Login

Test: Group Theory - 3


20 Questions MCQ Test Topic-wise Tests & Solved Examples for IIT JAM Mathematics | Test: Group Theory - 3


Description
This mock test of Test: Group Theory - 3 for Mathematics helps you for every Mathematics entrance exam. This contains 20 Multiple Choice Questions for Mathematics Test: Group Theory - 3 (mcq) to study with solutions a complete question bank. The solved questions answers in this Test: Group Theory - 3 quiz give you a good mix of easy questions and tough questions. Mathematics students definitely take this Test: Group Theory - 3 exercise for a better result in the exam. You can find other Test: Group Theory - 3 extra questions, long questions & short questions for Mathematics on EduRev as well by searching above.
QUESTION: 1

 If N is a set of natural numbers, then under binary operation  a · b = a + b, (N, ·) is

Solution:

QUESTION: 2

The number of generators in cyclic group of order 10 are

Solution:
QUESTION: 3

The set of all positive rational numbers forms an abelian group under the composition defined by

Solution:
QUESTION: 4

Set (1,2,3,4} is a finite abelian group of order... under multiplication modulo ... as composition.
Solution:
QUESTION: 5

Let G be a group of order 7 and φ(x) = x4, x ∈ G. Then f is 
Solution:

A group of prime order must be cyclic and every cyclic group is abelian. Then we can show that φ: G → G s.t. φ(x) = xn is an isomorphism if 0(G) and n and are co-prime.

QUESTION: 6

HK is a sub-group of G iff
Solution:
QUESTION: 7

Check the correct statement.
Solution:
QUESTION: 8

If a, b ∈ G, a group, then b is conjugate to a, if there exist c ∈ G, such that
Solution:
QUESTION: 9

If H1 and H2 are two subgroups of G, then following is also a subgroups of G
Solution:
QUESTION: 10

If (G, *) is a group and for all a, b ∈ G, b-1 * a-1* b * a = e, then G is
Solution:
QUESTION: 11

Number of elements of the cyclic group of order 6 can be used as generators of the group are
Solution:

Here, 6 = 2 x 3

QUESTION: 12

The multiplicative group {1, -1} is a subgroup of the multiplicative group
Solution:
QUESTION: 13

A set G with a binary composition denoted multiplicative is a group, if
Solution:
QUESTION: 14

In the additive group of integers, the order of every elements a ≠  0 is
Solution:
QUESTION: 15

Let Z be a set of integers, then under ordinary multiplication (Z, ·) is
Solution:
QUESTION: 16

Set of all n, nth roots of unity from a finite abelian group of order n with respect to
Solution:
QUESTION: 17

The generators of a group G = {a, a2, a3, a4, a5, a6 = e) are
Solution:

we have o(G) = 6 and prime to 6 are 1 and 5

QUESTION: 18

If G is a group such that a2 = e, for all a ∈ G, then G is
Solution:
QUESTION: 19

If f = (2,3) and g = (4, 5) are two permutation on 1,2,3,4,5 then fg is
Solution:

we have f(g) = (2, 3) (45)

0 is the identity element of G and 2 +5 2 +5 2 +5 2 +5 2 = 0

QUESTION: 20

If G is a group, then for all a, b ∈ G
Solution:

Recommended Content

Recommended Tests

Similar Content

Related tests
Follow Us
© EduRev