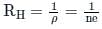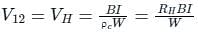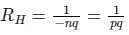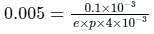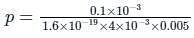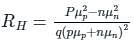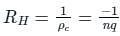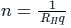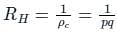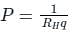Test: Hall Effect - Electronics and Communication Engineering (ECE) MCQ
10 Questions MCQ Test Electronic Devices - Test: Hall Effect
For which one of the following materials, is the Hall coefficient closest to zero?
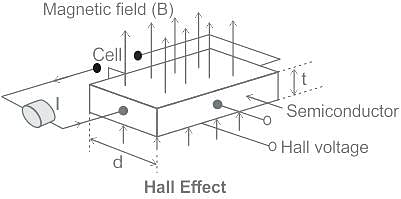
In Hall effect, a difference voltage is produced _______ to electric current in the conductor, and to an applied _____ field perpendicular to the current.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Calculate the hall voltage when the magnetic field is 8 A/m, current is 4 A, width is 5 m and the concentration of carrier is 1020.
For an n-type Ge specimen, width = 4 mm, length = 1 mm, current (along the length of specimen) = 1 mA, magnetic field (perpendicular to the current flow direction) = 0.1 Wb/m2 and Hall voltage magnitude = 0.005 V. Calculate the majority carriers density.
For a particular material, the Hall coefficient is found to be zero. The material is
Calculate the Hall Effect coefficient when number of electrons in a semiconductor is 1020.
What is the conductivity when the Hall Effect coefficient is 5 and mobility is 5cm2 /s.
|
21 docs|29 tests
|
|
21 docs|29 tests
|