Test: Hyperbola- 3 - Commerce MCQ
15 Questions MCQ Test Online MCQ Tests for Commerce - Test: Hyperbola- 3
Variable circles are drawn touching two fixed circles externally then locus of centre of variable circle is
The locus of the mid points of the chords passing through a fixed point (a, b) of the hyperbola, 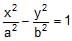 is
is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The locus of the foot of the perpendicular from the centre of the hyperbola xy = c2 on a variable tangent is
The equation to the chord joining two points (x1, y1) and (x2, y2) on the rectangular hyperbola xy = c2 is
The equation 9x2 - 16y2 - 18x + 32y - 15 = 0 represent a hyperbola
From the points of the circle x2 + y2 = a2, tangents are drawn to the hyperbola x2 – y2 = a2; then the locus of the middle points of the chords of contact is
The tangent to the hyperbola xy = c2 at the point P intersects the x-axis at T and the y-axis at T'. The normal to the hyperbola at P intersects the x-axis at N and the y-axis at N'. The areas of the triangles PNT and PNT' are D and D' respectively, then is
The asymptote of the hyperbola form with any tangent to the hyperbola a triangle whose area is a2 tan l in magnitude then its eccentricity is
From any point on the hyperbola H1 : (x2/a2) - (y2/b2) = 1 tangents are drawn to the hyperbola .H2 : (x2/a2) - (y2/b2) = 2. The area cut-off by the chord of contact on the asymptotes of H2 is equal to
The tangent at P on the hyperbola (x2 / a2) - (y2 / b2) = 1 meets the asymptote at Q. If the locus of the mid point of PQ has the equation (x2 / a2) - (y2 / b2) = k, then k has the value equal to
The tangent to the hyperbola, x2 - 3y2 = 3 at the point (√3, 0) when associated with two asymptotes constitutes.
If θ is the angle between the asymptotes of the hyperbola with eccentricity e, then sec θ/2 can be
If (5, 12) and (24, 7) are the focii of a conic passing through the origin then the eccentricity of conic is
The point of contact of 5x + 12y = 19 and x2 – 9y2 = 9 will lie on
Equation (2 + λ)x2 - 2λxy + (λ - 1)y2 - 4x - 2 = 0 represents a hyperbola if
|
705 tests
|

















