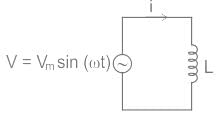
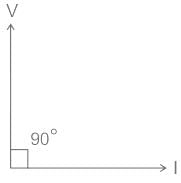
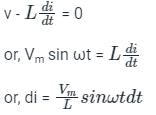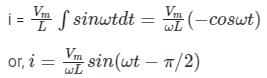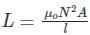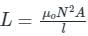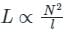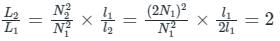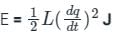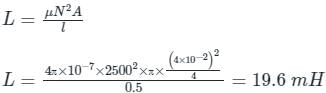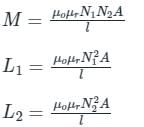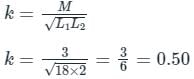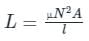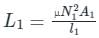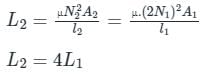Test: Inductance - 1 - Electrical Engineering (EE) MCQ
10 Questions MCQ Test - Test: Inductance - 1
What is the power dissipation (in W) in an ideal inductor having an inductance of 0.2 H?
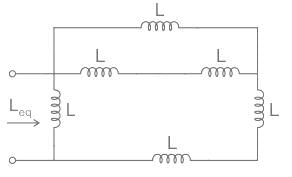
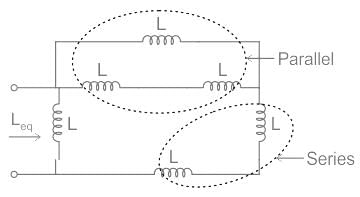
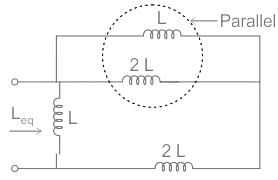
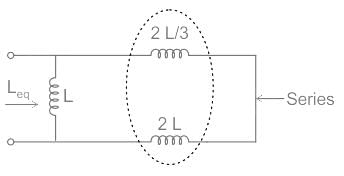
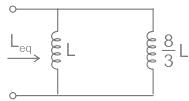
Consider the image given below. According to the image, find out the value of Leq if L is 22 mH.


Two coils in differential connection have a self-inductance of 2 mH and 4 mH and mutual inductance of 0.15 mH. The equivalent inductance of the series opposing combination will be:
If both the number of turns and core length of an inductive coil are doubled, then its self inductance will be
The energy stored in a coil with inductance L is determined as:
Inductance of a solenoid of 2500 turns wound uniformly over a length of 0.5 m cylindrical paper tube of 4 cm diameter in air medium is around:
Two coils having self-inductance of 18 H and 2 H, respectively, are magnetically coupled and the mutual inductance between them is 3 H. Find the value of coefficient of coupling.
If the number of turns in a coil is doubled in the same length and area, the inductance L will
If a brass core of an inductor is replaced by an iron core, the inductance of coil: