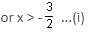CAT Exam > CAT Tests > Daily Test for CAT Preparation > Test: Inequalities (April 16) - CAT MCQ
Test: Inequalities (April 16) - CAT MCQ
Test Description
10 Questions MCQ Test Daily Test for CAT Preparation - Test: Inequalities (April 16)
Test: Inequalities (April 16) for CAT 2025 is part of Daily Test for CAT Preparation preparation. The Test: Inequalities (April 16) questions and answers have been
prepared according to the CAT exam syllabus.The Test: Inequalities (April 16) MCQs are made for CAT 2025 Exam. Find important
definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Test: Inequalities (April 16) below.
Solutions of Test: Inequalities (April 16) questions in English are available as part of our Daily Test for CAT Preparation for CAT & Test: Inequalities (April 16) solutions in
Hindi for Daily Test for CAT Preparation course. Download more important topics, notes, lectures and mock
test series for CAT Exam by signing up for free. Attempt Test: Inequalities (April 16) | 10 questions in 20 minutes | Mock test for CAT preparation | Free important questions MCQ to study Daily Test for CAT Preparation for CAT Exam | Download free PDF with solutions
Test: Inequalities (April 16) - Question 1
N is a negative real number. Which of the following is not true?
Detailed Solution for Test: Inequalities (April 16) - Question 1
Test: Inequalities (April 16) - Question 2
The number of solutions of the equation |x2 - 4| = 4 + x2 is
Detailed Solution for Test: Inequalities (April 16) - Question 2
Detailed Solution for Test: Inequalities (April 16) - Question 3
Test: Inequalities (April 16) - Question 4
A, B, C and D are four friends and they are having w, x, y and z amount, respectively, such that w - z > 0, x - z < 0 and y - z < 0. Which of the following is necessarily true?
Detailed Solution for Test: Inequalities (April 16) - Question 4
Test: Inequalities (April 16) - Question 5
If a < b, then the solution of x2 - (a + b) x + ab < 0 is
Detailed Solution for Test: Inequalities (April 16) - Question 5
Test: Inequalities (April 16) - Question 6
What values of 'm' satisfy the inequality 3m2 - 21m + 30 < 0?
Detailed Solution for Test: Inequalities (April 16) - Question 6
Test: Inequalities (April 16) - Question 7
What is the best description of 'x' which satisfies the inequality x2 - 5x + 6 ≤ 0 ?
Detailed Solution for Test: Inequalities (April 16) - Question 7
Detailed Solution for Test: Inequalities (April 16) - Question 8
Test: Inequalities (April 16) - Question 9
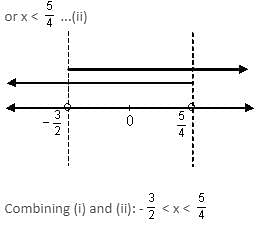
Solve the system of inequalities:
5x + 2 > 3x - 1
3x + 1 > 7x - 4
Detailed Solution for Test: Inequalities (April 16) - Question 9
Detailed Solution for Test: Inequalities (April 16) - Question 10
|
152 docs|327 tests
|
Information about Test: Inequalities (April 16) Page
In this test you can find the Exam questions for Test: Inequalities (April 16) solved & explained in the simplest way possible.
Besides giving Questions and answers for Test: Inequalities (April 16), EduRev gives you an ample number of Online tests for practice