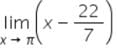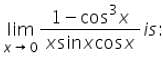Test: Introduction And Algebra Of Limits - JEE MCQ
10 Questions MCQ Test Mathematics (Maths) for JEE Main & Advanced - Test: Introduction And Algebra Of Limits
If the right and left hand limits coincide, we call that common value as the limit of f(x) at x = a and denote it by
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
For the limit of a function to exist we must have
Let f be any function, such that 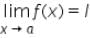 exists, then
exists, then 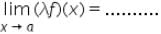
Let f(x) and g(x) be two function, such that 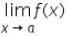 and
and 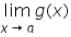 exists, then the limit of the product of the function f(x) and g(x) is given by
exists, then the limit of the product of the function f(x) and g(x) is given by
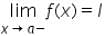 is the expected value of f at x = a given the values of f near x to the left of a. This value is called the……….of f at a.
is the expected value of f at x = a given the values of f near x to the left of a. This value is called the……….of f at a.
As x → a, f(x) → l, then l is called the……..of the function f(X) which is symbolically written as…….
Consider the function f(x) = x + 10. Let us compute the value of the function f(x) for x very near to 5. Some of the points near and to the left of 5 and right to the 5 are given in the table.

|
209 videos|443 docs|143 tests
|
|
209 videos|443 docs|143 tests
|