Test: Introduction & Properties of Fluid Level- 2 - Mechanical Engineering MCQ
15 Questions MCQ Test Fluid Mechanics for Mechanical Engineering - Test: Introduction & Properties of Fluid Level- 2
In general decrease in temperature, results in
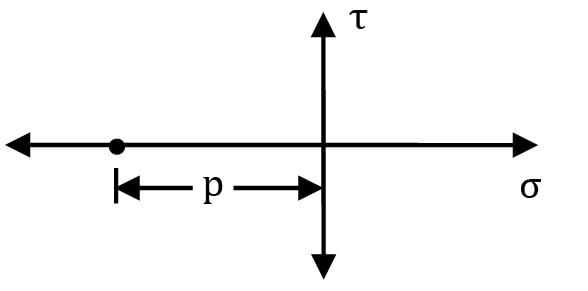
What is the radius of Mohr’s stress (in kPa) circle for a point inside a fluid mass which rotates like a solid body in a cylindrical container. The pressure at the point is 200 kPa.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Which one of the following is the bulk modulus K of a fluid? (Symbols have the usual meaning)
If angle of contact of a drop of liquid is acute, then
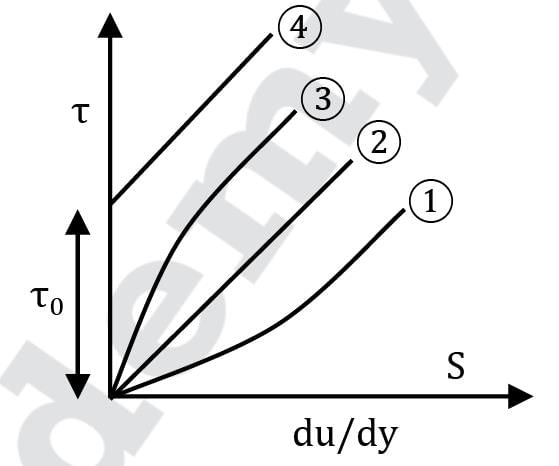
Which of the following fluids exhibit a certain shear stress at zero shear strain rate followed by a straight line relationship between shear stress and shear strain rate?
An increase in pressure of a liquid from 7.5 MPa to 15 MPa results into 0.2 percent decrease in its volume. The coefficient of compressibility of the liquid in m2/N is
If the surface tension of water-air interface is 0.073 N/m, the gauge pressure inside a rain drop of 1 mm diameter will be
Group I contains the types of fluids while Group II contains the shear stress - rate of shear relationship of different types of fluids, as shown in the figure.

The vapour pressure is the characteristic fluid property involved in the phenomenon of
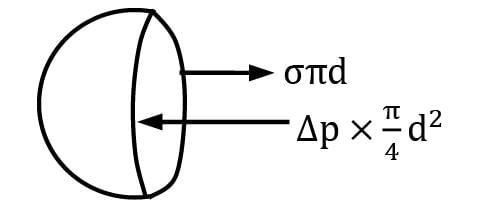
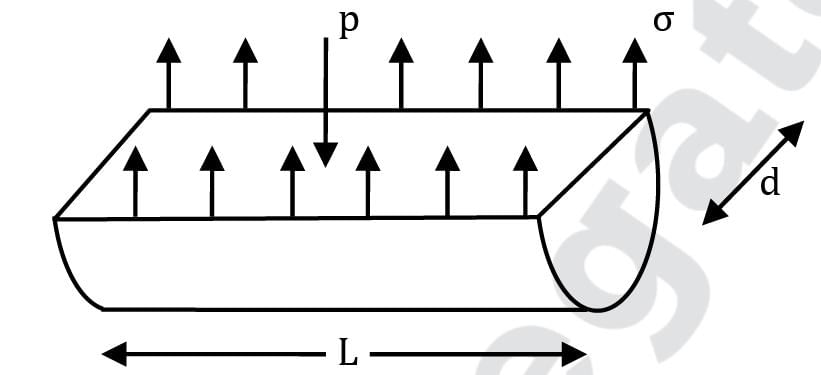
The absolute pressure inside a liquid jet is slightly greater than the atmospheric pressure. This excess pressure (p), the surface tension (σ) of the liquid and diameter (d) of jet are related as
The Mohr’s stress circle for any point considered inside a fluid at rest is given as
With increase in pressure, the bulk modulus of elasticity for an ideal gas
Assertion (A): An open glass tube is dipped in mercury. The mercury level inside the tube shall rise above the level of mercury outside.
Reason (R): The cohesive force between the molecules of mercury is greater than the adhesive force between mercury and glass.
Which of the following dimensionless no. represents applicability of concept of continuum analysis of a system?
The density of water is maximum at a temperature of
|
56 videos|104 docs|75 tests
|
|
56 videos|104 docs|75 tests
|